
分析 (Ⅰ)利用三种方程的转化方法,即可求曲线C1与曲线C2的参数方程
(Ⅱ)若点A,B分别在曲线C1与曲线C2上,求|AB|的最小值,即求出A到曲线C2距离的最小值.
解答 解:(Ⅰ)曲线C1的直角坐标方程为(x+1)2+(y-1)2=1,参数方程为$\left\{\begin{array}{l}{x=-1+cosα}\\{y=1+sinα}\end{array}\right.$(α为参数);
曲线C2的极坐标方程为ρcos(θ+$\frac{π}{4}$)=2$\sqrt{2}$,直角坐标方程为x-y-4=0,参数方程为$\left\{\begin{array}{l}{x=4+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数);
(Ⅱ)设A(-1+cosα,1+sinα),
A到曲线C2的距离d=$\frac{|-1+cosα-1-sinα-4|}{\sqrt{2}}$=$\frac{6+\sqrt{2}sin(α-45°)}{\sqrt{2}}$,
∴sin(α-45°)=-1时,|AB|的最小值为3$\sqrt{2}$-1.
点评 本题考查三种方程的转化,考查点到直线距离公式的运用,考查学生的计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
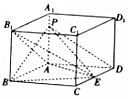 如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )
如图,在长方体ABCD-A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1,F是棱DD1与平面BEP的交点,则DF的长为( )| A. | 1 | B. | $\frac{8}{9}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{10}$ | B. | -$\frac{π}{5}$ | C. | $\frac{π}{10}$ | D. | $\frac{π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a>b”是“a2>b2”的充分不必要条件 | |
| B. | 命题“?x0∈R,$x_0^2+1<0$”的否定是“?x∈R,x2+1>0” | |
| C. | 关于x的方程x2+(a+1)x+a-2=0的两实根异号的充要条件是a<1 | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2 018×2 014 | B. | 2 018×2 013 | C. | 1 011×2 015 | D. | 1 010×2 012 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
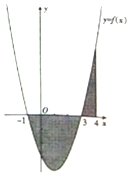
| A. | $\int_{-1}^4{f(x)}dx$ | B. | $-\int_{-1}^4{f(x)}dx$ | ||
| C. | $\int_3^4{f(x)}dx-\int_{-1}^3{f(x)dx}$ | D. | $\int_{-1}^3{f(x)}dx-\int_3^4{f(x)dx}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com