
���� ��1����С������Ϊ�¼�A������n���ظ��������¼�Aǡ�÷���k�εĸ��ʼ��㹫ʽ�����С������ľ��˾����ĸ��ʣ�
��2�������������ο���ȡֵΪ��-3��-2��4��5���ֱ������Ӧ�ĸ��ʣ��ɴ�������ε���ѧ������������ҷ��������Ӷ��õ���ľ��˾ѡ�ü���������ľ�ֵ����
��� �⣺��1����С������Ϊ�¼�A��
��$P��A��=C_3^2{��\frac{2}{3}��^2}\frac{1}{3}+{��\frac{2}{3}��^3}=\frac{20}{27}$��
����С������ľ��˾����ĸ���Ϊ$\frac{20}{27}$������5�֣�
��2�������������ο���ȡֵΪ��-3��-2��4��5������6�֣�
$P����=-3��=C_3^1{��\frac{1}{3}��^2}\frac{2}{3}+{��\frac{1}{3}��^3}=\frac{7}{27}$��
$P����=-2��=C_3^2{��\frac{2}{3}��^2}\frac{1}{3}•\frac{1}{3}=\frac{4}{27}$��
$P����=4��=C_3^2{��\frac{2}{3}��^2}\frac{1}{3}•\frac{2}{3}=\frac{8}{27}$��
$P����=5��={��\frac{2}{3}��^3}=\frac{8}{27}$��
��εķֲ���Ϊ��
| �� | -3 | -2 | 4 | 5 |
| P | $\frac{7}{27}$ | $\frac{4}{27}$ | $\frac{8}{27}$ | $\frac{8}{27}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��м���ѧ��������Ӧ�ã����е��⣬������߿��ж��DZؿ�����֮һ��


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | -5 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | an+1=an+n��n��N* | B�� | an=an-1+n��n��N*��n��2 | ||
| C�� | an+1=an+��n+1����n��N*��n��2 | D�� | an=an-1+��n-1����n��N*��n��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
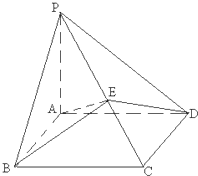 ��ͼ��������P-ABCD�У�PA��ƽ��ABCD���ı���ABCDΪƽ���ı��Σ�AB=1��BC=$\sqrt{2}$����ABC=45�㣬AE��PC������ΪE��
��ͼ��������P-ABCD�У�PA��ƽ��ABCD���ı���ABCDΪƽ���ı��Σ�AB=1��BC=$\sqrt{2}$����ABC=45�㣬AE��PC������ΪE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{2}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{��}{4}$ | D�� | $\frac{��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���ⳤΪ2��������ABCD-A1B1C1D1�У�E��F�ֱ�ΪA1B1��CD���е㣮
���ⳤΪ2��������ABCD-A1B1C1D1�У�E��F�ֱ�ΪA1B1��CD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com