
分析 求出被积函数,由定积分公式求出a,求出二项式的通项公式,化简整理,令9-2r=3,求出r,即可得到所求系数.
解答 解:a=${∫}_{0}^{\frac{π}{2}}$(-cosx)dx=-sinx|${\;}_{0}^{\frac{π}{2}}$
=-(sin$\frac{π}{2}$-sin0)=-1,
则(-x-$\frac{1}{2x}$)9展开式中的通项公式为${C}_{9}^{r}$(-x)9-r(-$\frac{1}{2x}$)r
=-($\frac{1}{2}$)r${C}_{9}^{r}$x9-2r,r=0,1,…,9,
由9-2r=3,可得r=3,
x3项的系数为-($\frac{1}{2}$)3${C}_{9}^{3}$=-$\frac{21}{2}$.
故答案为:-$\frac{21}{2}$.
点评 本题考查定积分的运算和二项式定理的运用:求指定项的系数,考查运算能力,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
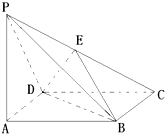 如图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,PA=a,E为CP中点,
如图,四棱锥P-ABCD的底面是边长为a的正方形,PA⊥平面ABCD,PA=a,E为CP中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{3},\frac{{\sqrt{3}}}{2}-\frac{π}{6})$ | B. | $(-\frac{π}{3},\frac{π}{6}-\frac{{\sqrt{3}}}{2})$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com