
| A. | 16 | B. | 28 | C. | 40 | D. | 56 |
分析 按连续值班天数和第一天是否值班分类,使用排列数公式计算.
解答 解:(1)若连续值班天数为1,3,3,或2,2,3,且有连续两天不值班,则不同的值班方法为2×2×$\frac{{A}_{3}^{3}}{{A}_{2}^{2}}$=12,
(2)若连续值班天数为1,3,3,或2,2,3,且在1号或10号不值班,则不同的值班方法为2×2×$\frac{{A}_{3}^{3}}{{A}_{2}^{2}}$=12,
(3)若连续值班天数为1,1,2,3或2,2,2,1,则不同的值班方法为$\frac{{A}_{4}^{4}}{{A}_{2}^{2}}$+$\frac{{A}_{4}^{4}}{{A}_{3}^{3}}$=12+4=16,
综上,所有不同的值班方法共有12+12+16=40种方法,
故选C.
点评 本题考查了排列数公式的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 男生 | 15 | 35 | 50 |
| 女生 | 30 | 40 | 70 |
| 总计 | 45 | 75 | 120 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )
如图,由两条曲线y=-x2,4y=-x2及直线y=-1所围成的图形的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{\begin{array}{l}8\end{array}}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
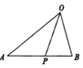 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com