
分析 通过an=n•3n+1-2•3n,分别计算出{n•3n+1}、{2•3n}的前n项和,进而可得结论.
解答 解:an=3n•(3n-2)=n•3n+1-2•3n,
记Qn=1•32+2•33+…+n•3n+1,
则3Qn=1•33+2•34+…+(n-1)•3n+1+n•3n+2,
∴-2Qn=32+33+34+…+3n+1-n•3n+2=$\frac{{3}^{2}(1-{3}^{n})}{1-3}$-n•3n+2=$(\frac{1}{2}-n)$•3n+2-$\frac{9}{2}$,
即Qn=$\frac{2n-1}{4}$•3n+2+$\frac{9}{4}$,
∴Sn=1•32+2•33+…+n•3n+1-2(3+32+33+…+3n)
=$\frac{2n-1}{4}$•3n+2+$\frac{9}{4}$-2•$\frac{3(1-{3}^{n})}{1-3}$
=$\frac{6n-7}{4}$•3n+1+$\frac{21}{4}$.
点评 本题考查求数列通项,考查运算求解能力,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
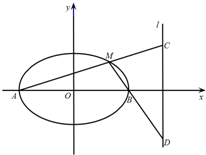 已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.
已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x=k•180°,k∈Z} | B. | {x|x=k•180°+90°,k∈Z} | ||
| C. | {x|x=k•360°,k∈Z} | D. | {x|x=k•360°+90°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a>b | B. | a<b | ||
| C. | a=b | D. | a,b的大小关系不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com