
分析 直接利用类比推理,即可得出结论.
解答 解:由cosx=0有无穷多个根:±$\frac{1}{2}$π,±$\frac{3}{2}$π,…,
可得:cosx=(1-$\frac{{x}^{2}}{\frac{1}{4}{π}^{2}}$)(1-$\frac{{x}^{2}}{\frac{9}{4}{π}^{2}}$)…,把这个式子的右边展开,发现x2的系数为$\frac{1}{\frac{1}{4}{π}^{2}}$+$\frac{1}{\frac{9}{4}{π}^{2}}$+…=$\frac{1}{2}$,
即$\frac{1}{{1}^{2}}$+$\frac{1}{{3}^{2}}$+…=$\frac{{π}^{2}}{8}$.
故答案为$\frac{1}{{1}^{2}}$+$\frac{1}{{3}^{2}}$+…=$\frac{{π}^{2}}{8}$.
点评 本题考查的知识点是类比推理,考查学生的计算能力,难度较大.


科目:高中数学 来源: 题型:选择题
 函数f(x)=sin(ωx+φ)(其中ω>0且|φ|≤$\frac{π}{2}$)的图象如图所示,为了得到y=sinωx的图象,只需把y=f(x)的图象上所有点( )
函数f(x)=sin(ωx+φ)(其中ω>0且|φ|≤$\frac{π}{2}$)的图象如图所示,为了得到y=sinωx的图象,只需把y=f(x)的图象上所有点( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
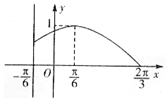 已知定义在区间[-π,$\frac{2}{3}$π]上的函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}<φ<\frac{π}{2}$)的图象关于直线x=-$\frac{π}{6}$对称,当x∈$[-\frac{π}{6},\frac{2π}{3}]$时,f(x)的图象如图所示.
已知定义在区间[-π,$\frac{2}{3}$π]上的函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}<φ<\frac{π}{2}$)的图象关于直线x=-$\frac{π}{6}$对称,当x∈$[-\frac{π}{6},\frac{2π}{3}]$时,f(x)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
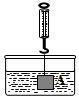 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则如图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )
在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则如图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )| A. | 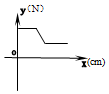 | B. | 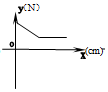 | C. |  | D. | 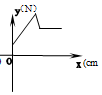 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com