
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �٢ڢ� |
���� ���ݡ������������Ķ��壬��Ϻ��������Ե����ʷֱ�����жϼ��ɵõ����ۣ�
��� �⣺�٣���f��0��=1��f��x��+f��1-x��=1��
��f��0��+f��1��=1����f��1��=0��
���?x��[0��1]�����ݡ������������Ķ���֪f��x����f��1��=0���ʢ���ȷ��
�ڡߵ�x��[0��$\frac{1}{4}$]ʱ��f��x����-2x+1�������
�൱x=$\frac{1}{4}$ʱ��f��$\frac{1}{4}$����-2��$\frac{1}{4}$+1=$\frac{1}{2}$��
��f��x��+f��l-x��=l����f��$\frac{1}{2}$��=$\frac{1}{2}$��
�ɶ�$\frac{1}{4}$��$\frac{1}{2}$���ɡ������������Ķ����֪��f��$\frac{1}{4}$����$\frac{1}{2}$��
����f��$\frac{1}{4}$��=$\frac{1}{2}$��
ͬ����f��$\frac{3}{4}$��=$\frac{1}{2}$��
��x��[$\frac{1}{4}$��$\frac{3}{4}$]ʱ���ɡ������������Ķ����֪��f��$\frac{1}{4}$����f��x����f��$\frac{3}{4}$������f��x��=$\frac{1}{2}$�����Ԣڲ���ȷ��
���ɢ��У���x��[$\frac{1}{4}$��$\frac{3}{4}$]ʱ��f��x��=$\frac{1}{2}$���ɵã�f��$\frac{5}{11}$��=f��$\frac{7}{13}$��=$\frac{1}{2}$��
��f��x��+f��1-x��=1�ã�f��$\frac{1}{8}$��+f��$\frac{7}{8}$��=1��
��f��$\frac{1}{8}$��+f��$\frac{5}{11}$��+f��$\frac{7}{13}$��+f��$\frac{7}{8}$��=2���ʢ���ȷ��
����ȷ�����У��٢ۣ�
��ѡ��C��
���� ���⿼�������������ж������ã��漰�����������ʣ����������Ե�Ӧ�ã���ȷ�����¶����ǽ������Ĺؼ�����������ѧ���ij���˼ά�������ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���� | ������ | �ܼ� | |
| ���� | 40 | 20 | 60 |
| �� | 20 | 30 | 50 |
| �ܼ� | 60 | 50 | 110 |
| P��K2��k�� | 0.500 | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |
| A�� | 90% | B�� | 95% | C�� | 99% | D�� | 99.9% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | e | B�� | $\frac{1}{2}$ | C�� | $\sqrt{2}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
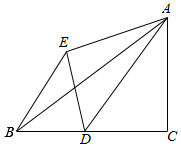 ��ͼ����ABC�У���C=90�㣬AC=6��BC=8����D�ӵ�C��������ÿ��1����λ���ٶ�����CB���B�˹�����ADE�͡�ADC����AD����Գƣ�����BE�����D�˶�ʱ��Ϊt�룮
��ͼ����ABC�У���C=90�㣬AC=6��BC=8����D�ӵ�C��������ÿ��1����λ���ٶ�����CB���B�˹�����ADE�͡�ADC����AD����Գƣ�����BE�����D�˶�ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�e�� | B�� | ��-�ޣ�e] | C�� | ��-�ޣ�$\frac{1}{e}$�� | D�� | ��-�ޣ�$\frac{1}{e}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\sqrt{3}$ | C�� | 5 | D�� | $\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com