
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 经过椭圆
经过椭圆![]() 的右焦点且与圆
的右焦点且与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且交椭圆
,且交椭圆![]() 于
于![]() 两点,射线
两点,射线![]() 于椭圆
于椭圆![]() 交于点
交于点![]() ,设
,设![]() 的面积于
的面积于![]() 的面积分别为
的面积分别为![]() .
.
①求![]() 的最大值;
的最大值;
②当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据离心率为![]() 、圆心到直线距离等于半径,结合性质
、圆心到直线距离等于半径,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的方程;(2) 直线
的方程;(2) 直线![]() 与圆
与圆![]() 相切得:
相切得: 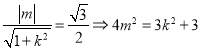 ,将直线
,将直线![]() 代入椭圆
代入椭圆![]() 的方程得:
的方程得: ![]() ①根据点到直线距离公式、弦长公式结合韦达定理及三角形面积公式可得
①根据点到直线距离公式、弦长公式结合韦达定理及三角形面积公式可得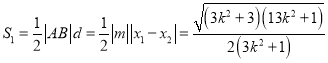 ,利用基本不等式可得结果;②当
,利用基本不等式可得结果;②当![]() 取得最大值时,
取得最大值时, ![]() ,
,  .
.
试题解析:(1)依题直线![]() 的斜率
的斜率![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,
,
依题有: 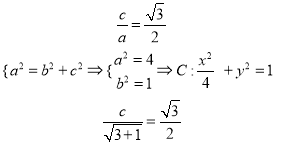
(2)由直线![]() 与圆
与圆![]() 相切得:
相切得: 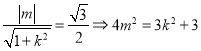 .
.
设![]() .将直线
.将直线![]() 代入椭圆
代入椭圆![]() 的方程得:
的方程得: ![]()
![]() ,且
,且![]() .
.![]()
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,故
,故![]() 的面积为:
的面积为:
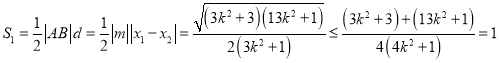 ,
,
当![]() .等号成立.故
.等号成立.故![]() 的最大值为1.
的最大值为1.
设![]() ,由直线
,由直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,可得
,可得![]() ,
,
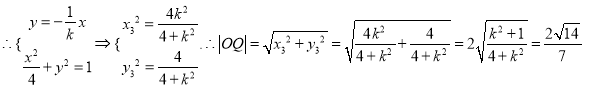 .
.
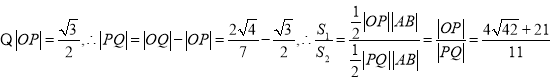 .,
.,
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形面积最值的.


科目:高中数学 来源: 题型:
【题目】某校为保证学生夜晚安全,实行教师值夜班制度,已知![]() 共5名教师每周一到周五都要值一次夜班,每周如此,且没有两人同时值夜班,周六和周日不值夜班,若
共5名教师每周一到周五都要值一次夜班,每周如此,且没有两人同时值夜班,周六和周日不值夜班,若![]() 昨天值夜班,从今天起
昨天值夜班,从今天起![]() 至少连续4天不值夜班,
至少连续4天不值夜班, ![]() 周四值夜班,则今天是周___________.
周四值夜班,则今天是周___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=x-(a+1)ln x-![]() (a∈R),g (x)=
(a∈R),g (x)=![]() x2+ex-xex.
x2+ex-xex.
(1)当x∈[1,e] 时,求f (x)的最小值;
(2)当a<1时,若存在x1∈[e,e2],使得对任意的x2∈[-2,0],f (x1)<g (x2)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128 dm2,上、下两边各空2 dm,左、右两边各空1 dm.如何设计海报的尺寸,才能使四周空白面积最小?
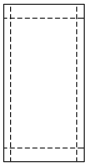
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() ).
).
(1)若点![]() 的直角坐标为
的直角坐标为![]() ,且点
,且点![]() 在曲线
在曲线![]() 内,求实数
内,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,当
,当![]() 变化时,求直线
变化时,求直线![]() 被曲线
被曲线![]() 截得的弦长的取值范围.
截得的弦长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 在区间
在区间![]() 上是单调函数,试求实数
上是单调函数,试求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,且
,且![]() ,若函数
,若函数![]() 在区间
在区间![]() 上恰有3个零点,求实数
上恰有3个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
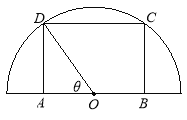
【题目】(本题满分15分)如图,在半径为![]() 的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为
的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为![]()
![]() .
.
(1)按下列要求建立函数关系式:
①设![]() ,将
,将![]() 表示为
表示为![]() 的函数;
的函数;
②设![]() (
(![]() ),将
),将![]() 表示为
表示为![]() 的函数;
的函数;
(2)请您选用(1)问中的一个函数关系,求圆柱形罐子的最大体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com