
【题目】(本题满分15分)如图,在半径为![]() 的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为
的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为![]()
![]() .
.
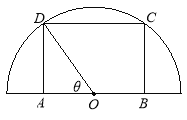
(1)按下列要求建立函数关系式:
①设![]() ,将
,将![]() 表示为
表示为![]() 的函数;
的函数;
②设![]() (
(![]() ),将
),将![]() 表示为
表示为![]() 的函数;
的函数;
(2)请您选用(1)问中的一个函数关系,求圆柱形罐子的最大体积.
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 经过椭圆
经过椭圆![]() 的右焦点且与圆
的右焦点且与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且交椭圆
,且交椭圆![]() 于
于![]() 两点,射线
两点,射线![]() 于椭圆
于椭圆![]() 交于点
交于点![]() ,设
,设![]() 的面积于
的面积于![]() 的面积分别为
的面积分别为![]() .
.
①求![]() 的最大值;
的最大值;
②当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自治区有甲、乙两位航模运动员参加了国家队集训,现分别从他们在集训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85
(I)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩中的位数;
(II)现要从中派一人参加国际比赛,从平均成绩和方差的角度考虑,你认为派哪位学生参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左右焦点分别为F1,F2,点P 在椭圆上运动,
的左右焦点分别为F1,F2,点P 在椭圆上运动, ![]() 的最大值为m,
的最大值为m, ![]() 的最小值为n,且m≥2n,则该椭圆的离心率的取值范围为________
的最小值为n,且m≥2n,则该椭圆的离心率的取值范围为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为坐标原点,焦点
的顶点为坐标原点,焦点![]() 在
在![]() 轴的正半轴上,过焦点
轴的正半轴上,过焦点![]() 作斜率为
作斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求抛物线![]() 的方程;
的方程;
(2)设点![]() ,直线
,直线![]() 分别交准线
分别交准线![]() 于点
于点![]() ,问:在
,问:在![]() 轴的正半轴上是否存在定点
轴的正半轴上是否存在定点![]() ,使
,使![]() ,若存在,求出定点
,若存在,求出定点![]() 的坐标,若不存在,试说明理由.
的坐标,若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com