
(本小题满分14分)如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A、B的一点.
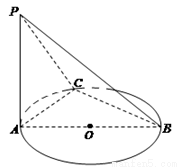
(1)求证:平面PAC⊥平面PBC;
(2)若PA=AB=2,∠ABC=30°,求三棱锥P-ABC的体积.
(1)(2)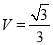
【解析】
试题分析:(1)由已知可得PA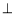 BC,AC
BC,AC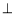 BC,再由直线与平面垂直的判定定理证得BC
BC,再由直线与平面垂直的判定定理证得BC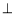 平面PAC,
平面PAC,
最后由平面与平面垂直的判定定理可得平面PAC⊥平面PBC
(2)∵PA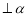 ,∴三棱锥P-ABC的体积
,∴三棱锥P-ABC的体积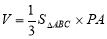 ,由已知PA=AB=2,∠ABC=30°可求
,由已知PA=AB=2,∠ABC=30°可求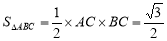 ,则体积可求.
,则体积可求.
试题解析:(1)设⊙O所在的平面为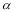 ,
,
依题意,PA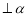 ,BC
,BC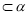 ,∴PA
,∴PA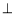 BC
BC
∵AB是⊙O的直径,C是圆周上不同于A、B的一点,∴AC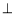 BC
BC
∵PA∩AC=A,∴BC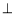 平面PAC
平面PAC
∵BC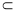 平面PBC,∴平面PAC⊥平面PBC
平面PBC,∴平面PAC⊥平面PBC
(2)∵PA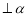 ,∴三棱锥P-ABC的体积
,∴三棱锥P-ABC的体积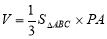
∵AB=2,∠ABC=30°,AC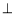 BC,∴AC=1,BC=
BC,∴AC=1,BC=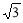
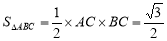
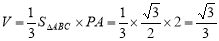
考点:直线与平面垂直的判定定理,平面与平面垂直的判定定理,椎体体积公式


科目:高中数学 来源:2014-2015学年上海市杨浦区高三上学期学业质量调研理科数学试卷(解析版) 题型:解答题
如图,有一块扇形草地OMN,已知半径为R, ,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN
,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN

(1)若点A为弧MN的一个三等分点,求矩形ABCD的面积S;
(2)当A在何处时,矩形ABCD的面积S最大?最大值为多少?
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省南京市、盐城市高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在直三棱柱 中,
中,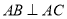 ,
, ,
,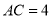 ,动点
,动点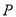 满足
满足 ,当
,当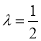 时,
时,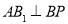 .
.
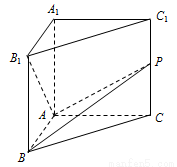
(1)求棱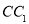 的长;
的长;
(2)若二面角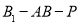 的大小为
的大小为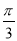 ,求
,求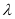 的值..
的值..
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省南京市、盐城市高三第一次模拟考试理科数学试卷(解析版) 题型:填空题
若一个圆锥的底面半径为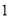 ,侧面积是底面积的
,侧面积是底面积的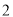 倍,则该圆锥的体积为 .
倍,则该圆锥的体积为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省江门市高三调研测试文科数学试卷(解析版) 题型:选择题
将正弦曲线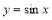 上所有的点横坐标伸长到原来的2倍,纵坐标不变,所得曲线对应的函数的最小正周期
上所有的点横坐标伸长到原来的2倍,纵坐标不变,所得曲线对应的函数的最小正周期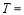
A.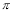 B.
B.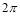 C.
C.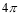 D.
D.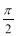
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com