
 某海域的东西方向上分别有A,B两个观测点(如图),它们相距5(3+$\sqrt{3}$)海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船,其航行速度为30海里/小时.
某海域的东西方向上分别有A,B两个观测点(如图),它们相距5(3+$\sqrt{3}$)海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船,其航行速度为30海里/小时.分析 (Ⅰ)利用正弦定理,求出BD,
(Ⅱ)在△DCB中,利用余弦定理求出CD,根据速度求出时间.
解答 解:(Ⅰ)由题意知AB=5(3+$\sqrt{3}$)海里,
∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30)°=105°,…(2分)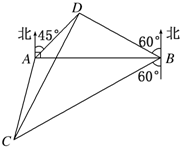
在△DAB中,由正弦定理得$\frac{DB}{sin∠DAB}$=$\frac{AB}{sin∠ADB}$,
∴DB=$\frac{AB•sin∠DAB}{sin∠ADB}$=$\frac{5(3+\sqrt{3})•sin45°}{sin105°}$
=$\frac{5(3+\sqrt{3})•sin45°}{sin45°cos60°+cos45°sin60°}$
=$\frac{5\sqrt{3}(\sqrt{3}+1)}{\frac{\sqrt{3}+1}{2}}$=10$\sqrt{3}$(海里) …(6分)
(Ⅱ)在△DBC中,∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,…(8分)
BC=20$\sqrt{3}$(海里),由余弦定理得
CD2=BD2+BC2-2BD•BC•cos∠DBC=300+1200-2×10$\sqrt{3}$×20$\sqrt{3}$×$\frac{1}{2}$=900,…(10分)
∴CD=30(海里),则需要的时间t=$\frac{30}{30}$=1(小时).…(11分)
答:救援船到达D点需要1小时.…(12分)
点评 本题考查正弦定理以及余弦定理的应用,解三角形的实际问题的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
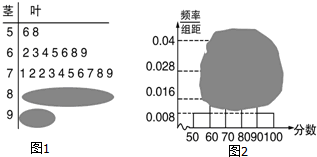
| A. | 25,2 | B. | 25,4 | C. | 24,2 | D. | 24,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com