
分析 (1)利用递推式即可得出;
(2)利用等比数列的前n项和公式即可得出.
解答 解:(1)∵Sn=$\frac{3}{2}$n2+$\frac{7}{2}$n,
∴当n=1时,a1=$\frac{3}{2}+\frac{7}{2}$=5,
当n≥2时,an=Sn-Sn-1=$\frac{3}{2}$n2+$\frac{7}{2}$n-$[\frac{3}{2}(n-1)^{2}+\frac{7}{2}(n-1)]$=3n+2.
当n=1时上式成立,∴an=3n+2(n∈N*).
(2)${a}_{{2}^{n}}$=3×2n+2.
∴此数列的前n项和Gn=3×(2+22+23+…+2n)+2n
=$3×\frac{2({2}^{n}-1)}{2-1}$
=3×2n+1-6+2n.
点评 本题考查了递推式的应用、等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,$\frac{3}{2}$) | B. | (-$\frac{3}{2}$,$\frac{1}{2}$) | C. | (-1,1) | D. | (-∞,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
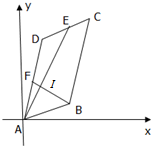 如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)
如图,已知平行四边形ABCD的顶点A(0,0),B(4,1),C(6,8)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | -10 | D. | -20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (0,+∞) | C. | (0,2) | D. | [0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com