
分析 (1)利用两角和与差的三角函数以及二倍角公式化简函数为一个角的一个三角函数的形式,通过周期公式求函数f(x)的周期,利用正弦函数的单调增区间求解函数的单调递增区间;
(2)通过函数f(x)的图象经过点(A,$\frac{1}{2}$),b,a,c成等差数列,求出A以及列出abc的关系,利用$\overrightarrow{AB}$•$\overrightarrow{AC}$=9,求出bc的值,通过余弦定理求a的值.
解答 解:(1)∵f(x)=sin($\frac{7π}{6}-2x$)-2sin2x+1
=-sin($\frac{π}{6}$-2x)-(1-cos2x)+1
=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x
=sin(2x+$\frac{π}{6}$),
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π;
由2k$π-\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解得单凋递增区间为:[kπ-$\frac{π}{3}$,k$π+\frac{π}{6}$],k∈Z…(6分)
(2)由f(A)=sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,可得:2A+$\frac{π}{6}$=$\frac{π}{6}$+2kπ或$\frac{5π}{6}$+2kπ(k∈Z),
∴A=$\frac{π}{3}$.…(8分)
又∵b,a,c成等差数列,
∴2a=b+c,…(9分)
而$\overrightarrow{AB}$•$\overrightarrow{AC}$=bccosA=$\frac{1}{2}bc$=9,
∴bc=18,…(10分)
∴cosA=$\frac{1}{2}$=$\frac{(b+c)^{2}-{a}^{2}}{2bc}$-1=$\frac{4{a}^{2}-{a}^{2}}{36}$-1=$\frac{{a}^{2}}{12}$-1,
∴a=3$\sqrt{2}$..…(12分)
点评 本题考查三角形的解法,两角和与差的三角函数以及二倍角公式的应用,三角函数的图象与性质,基本知识的考查.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,0) | D. | (-∞,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
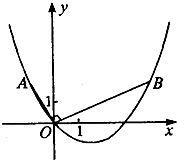 如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标 是(-1,2)
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标 是(-1,2)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,8) | C. | (4,8) | D. | [4,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com