练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知正数x，y满足：x+4y=xy，则x+y的最小值为9．

    分析 将x+4y=xy，转化为$\frac{4}{x}$+$\frac{1}{y}$=1，再由x+y=（x+y）（$\frac{4}{x}$+$\frac{1}{y}$）展开后利用基本不等式可求出x+y的最小值．

    解答 解：∵x＞0，y＞0，x+4y=xy，
    ∴$\frac{4}{x}$+$\frac{1}{y}$=1，
    ∴x+y=（x+y）（$\frac{4}{x}$+$\frac{1}{y}$）=5+$\frac{x}{y}$+$\frac{4y}{x}$≥5+2$\sqrt{\frac{x}{y}•\frac{4y}{x}}$=9，当且仅当x=2y取等号，结合x+4y=xy，
    解得x=6，y=3
    ∴x+y的最小值为9，
    故答案为：9．

    点评 本题考查基本不等式，应注意等号成立的条件；“1”的替换是一个常用的技巧，应学会灵活运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．河南省2013级高中学业水平考试在2015年1月16日至18日共考试三天，需考语文、数学、英语、物理、化学、生物、政治、历史、地理九门学科，若语文、数学、英语必须安排在下午，每天上午安排其余的六门学科，且每天上午考两门，下午考一门，问有多少种安排考试顺序的方法（　　）
    A．540B．720C．3240D．4320

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知i为虚数单位，复数z1=3-ai，z2=1+2i，若$\frac{{z}_{1}}{{z}_{2}}$复平面内对应的点在第四象限，则实数a的取值范围为$-6＜a＜\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

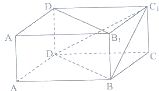
    9．如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，则点C到平面BC1D的距离等于（　　）
    A．$\sqrt{6}$B．$\frac{\sqrt{6}}{2}$C．$\frac{\sqrt{6}}{3}$D．$\frac{\sqrt{6}}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若a，b∈R，那么“a＜b＜0”是“$\frac{1}{a}＞\frac{1}{b}$”成立的（　　）
    A．充要条件B．充分不必要条件
    C．必要不充分条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图，抛物线C的顶点为坐标原点，焦点F为圆x2+（y-1）2=1的圆心．
    （Ⅰ）求抛物线C的方程；
    （Ⅱ）直线y=kx+2交圆F于A，B两点，线段AB的中点为M，直线MF交抛物线C于P，Q两点，且|PQ|=16|AB|，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．从集合A={1，2，3}，B={4，5，6}，C={7，8，9}中各取一个数，组成无重复数字的三位数的个数是162．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数f（x）=x2-1，则f（1）=（　　）
    A．1B．0C．-1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．求与椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$共焦点的抛物线的标准方程．

    查看答案和解析>>

    同步练习册答案