
【题目】已知几何体![]() ,其中四边形
,其中四边形![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为矩形,
为矩形, ![]() ,且
,且![]() ,
, ![]() .
.
(1)试判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,请说明理由;
,请说明理由;
(2)若![]() ,求该几何体的表面积.
,求该几何体的表面积.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,根据三角形中位线定理以及梯形的性质可得四边形
,根据三角形中位线定理以及梯形的性质可得四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,由线面平行的判定定理可得结果;(2)先证明
,由线面平行的判定定理可得结果;(2)先证明![]() 平面
平面![]() ,又因为
,又因为![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,根据勾股定理可得
,根据勾股定理可得![]() ,进而得
,进而得![]() ,
, ![]() 为直角三角形, 结合四边形
为直角三角形, 结合四边形![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为矩形,进而可得结果.
为矩形,进而可得结果.
试题解析:(1)存在线段![]() 的中点
的中点![]() ,使得
,使得![]() 平面
平面![]() ,理由如下:
,理由如下:
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
,
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,且
,且![]() ,
,
又∵四边形![]() 为直角梯形,
为直角梯形, ![]() ,且
,且![]() ,
,
∴![]() ,
, ![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)因为四边形![]() 为直角梯形,
为直角梯形, ![]() ,且
,且![]() ,
, ![]() ,
,
所以![]() ,∴
,∴![]() .
.
又![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
所以![]() ,进而
,进而![]() .
.
所以![]() ,
,
因为![]() 为直角三角形,所以
为直角三角形,所以![]() ,
,
又四边形![]() 也为直角梯形,
也为直角梯形, ![]() ,
,
又![]() ,
, ![]() ,
,
所以该几何体的表面积为![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】中国的钨矿资源储量丰富,在全球已经探明的钨矿产资源储量中占比近![]() ,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当
,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得部分数据如表.
.测得部分数据如表.
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式y=![]()
(2)求函数![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,PA=2,∠ABC=90°,![]() ,BC=1,
,BC=1, ![]() ,∠ACD=60°,E为CD的中点.
,∠ACD=60°,E为CD的中点.

(1)求证:BC∥平面PAE;
(2)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题α:函数![]() 的定义域是R;命题β:在R上定义运算:xy=x(1-y).不等式(x-a)(x+a)<1对任意实数x都成立.
的定义域是R;命题β:在R上定义运算:xy=x(1-y).不等式(x-a)(x+a)<1对任意实数x都成立.
(1)若α、β中有且只有一个真命题,求实数a的取值范围;
(2)若α、β中至少有一个真命题,求实数a的取值范围;
(3)若α、β中至多有一个真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为![]() (
(![]() ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72![]() ,肚脐至足底长度为103
,肚脐至足底长度为103![]() ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中非毕业班学生人数分布情况如下表,为了了解这2000个学生的体重情况,从中随机抽取160个学生并测量其体重数据,根据测量数据制作了下图所示的频率分布直方图.
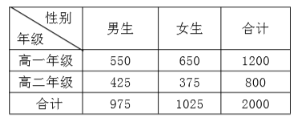

(1)为了使抽取的160个样品更具代表性,宜采取分层抽样,请你给出一个你认为合适的分层抽样方案,并确定每层应抽取的样品个数;
(2)根据频率分布直方图,求![]() 的值,并估计全体非毕业班学生中体重在
的值,并估计全体非毕业班学生中体重在![]() 内的人数;
内的人数;
(3)已知高一全体学生的平均体重为![]() ,高二全体学生的平均体重为
,高二全体学生的平均体重为![]() ,试估计全体非毕业班学生的平均体重.
,试估计全体非毕业班学生的平均体重.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 是等边三角形且垂直于底面
是等边三角形且垂直于底面![]() ,底面
,底面![]() 是矩形,
是矩形,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.
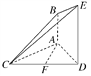
(1)求证:AF∥平面BCE;
(2)判断平面BCE与平面CDE的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,其离心率为
,其离心率为![]() ,以原点为圆心,椭圆的短轴长为直径的圆被直线
,以原点为圆心,椭圆的短轴长为直径的圆被直线![]() 截得的弦长等于
截得的弦长等于![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的左顶点,过点
的左顶点,过点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,过原点与
,过原点与![]() 平行的直线与椭圆相交于
平行的直线与椭圆相交于![]() 两点,问是否存在常数
两点,问是否存在常数![]() ,使
,使![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com