
已知四棱锥P-ABCD,底面ABCD是 ,边长为
,边长为 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.

(1)证明:DN//平面PMB;
(2)证明:平面PMB 平面PAD.
平面PAD.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)首先取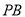 中点
中点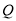 ,然后利用三角形中位线定理与平行四边形证明
,然后利用三角形中位线定理与平行四边形证明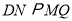 ,最后利用直线与平面平行的判定定理.(2)转化为证明
,最后利用直线与平面平行的判定定理.(2)转化为证明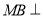 平面
平面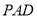 ,进而转化为证明
,进而转化为证明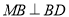 (由正三角形三线合一可证)和
(由正三角形三线合一可证)和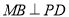 ,而证明
,而证明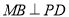 可转化为证明
可转化为证明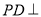 平面
平面 (已知).
(已知).
试题解析:(1)证明:取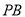 中点
中点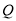 ,连结
,连结 ,
,

因为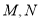 分别是棱
分别是棱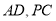 中点,所以
中点,所以 ,且
,且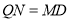 ,于是
,于是 .
.
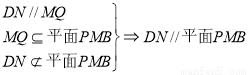 .
.
(2)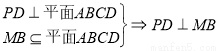
又因为底面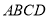 是
是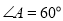 、边长为
、边长为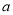 的菱形,且
的菱形,且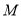 为
为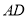 中点,
中点,
所以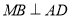 .
.
又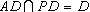 ,所以
,所以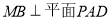 .
.

考点:1、直线与平面平行的判定及性质应用;2、平面与平面垂直的判定及性质应用.


科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:填空题
在椭圆 中,左焦点为
中,左焦点为 , 右顶点为
, 右顶点为 , 短轴上方端点为
, 短轴上方端点为 ,若
,若 ,则该椭圆的离心率为___________.
,则该椭圆的离心率为___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com