
分析 (Ⅰ)由题意画出图形,利用平面几何知识可得|EA|+|EB|=4,再由椭圆定义得点E的轨迹方程;
(Ⅱ)若直线ON的斜率不存在,可得|ON|=2$\sqrt{3}$,|OM|=2,|MN|=4,利用三角形面积相等可得原点O到直线MN的距离d=$\sqrt{3}$.若直线ON的斜率存在,设直线OM的方程为y=kx,代入椭圆方程,求得M坐标,直线ON的方程为y=$-\frac{1}{k}x$,代入y=$2\sqrt{3}$求得N的坐标.利用勾股定理求得|MN|2,再由三角形面积相等可得原点O到直线MN的距离d=$\sqrt{3}$.
解答 (Ⅰ)解:∵|AD|=|AC|,EB∥AC,故∠EBD=∠ACD=∠ADC,∴|EB|=|ED|,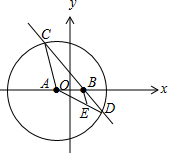
故|EA|+|EB|=|EA|+|ED|=|AD|.
又圆A的标准方程为(x+1)2+y2=16,从而|AD|=4,
∴|EA|+|EB|=4,
由题设得A(-1,0),B(1,0),|AB|=2,
由椭圆的定义可得点E的轨迹方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)证明:①若直线ON的斜率不存在,|ON|=2$\sqrt{3}$,|OM|=2,|MN|=4,
原点O到直线MN的距离d=$\frac{|OM|•|ON|}{|MN|}=\sqrt{3}$.
②若直线ON的斜率存在,设直线OM的方程为y=kx,代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,得${x}^{2}=\frac{12}{3+4{k}^{2}}$,${y}^{2}=\frac{12{k}^{2}}{3+4{k}^{2}}$,
直线ON的方程为y=$-\frac{1}{k}x$,代入y=$2\sqrt{3}$,得N($-2\sqrt{3}k,2\sqrt{3}$).
由题意知|MN|2=|ON|2+|OM|2=$(-2\sqrt{3}k)^{2}+(2\sqrt{3})^{2}+\frac{12(1+{k}^{2})}{3+4{k}^{2}}$=$\frac{48(1+{k}^{2})^{2}}{3+4{k}^{2}}$.
设原点O到直线MN的距离为d,由题意知|MN|•d=|OM|•|ON|,
得${d}^{2}=\frac{|OM{|}^{2}•|ON{|}^{2}}{|MN{|}^{2}}=3$,则d=$\sqrt{3}$.
综上所述,原点O到直线MN的距离为定值$\sqrt{3}$.
点评 本题考查曲线方程的求法,考查直线与椭圆位置关系的应用,考查计算能力,属中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:解答题
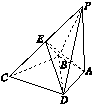 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosα-sinα | B. | sinα+cosα+2 | C. | sinα-cosα | D. | -sinα-cosα-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是菱形,$∠BAD=\frac{π}{3}$,PA=PD,F为AD的中点,PD⊥BF.
如图,四棱锥P-ABCD中,底面ABCD是菱形,$∠BAD=\frac{π}{3}$,PA=PD,F为AD的中点,PD⊥BF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 16种 | C. | 20种 | D. | 24种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com