
| A. | cosα-sinα | B. | sinα+cosα+2 | C. | sinα-cosα | D. | -sinα-cosα-2 |
分析 利用三角函数的恒等变换,三角函数在各个象限中的符号,化简所给的式子,可得结果.
解答 解:∵已知α为第三象限角,化简cosα$\sqrt{\frac{1+sinα}{1-sinα}}$-sinα$\sqrt{\frac{1+cosα}{1-cosα}}$
=cosα•|$\frac{1+sinα}{cosα}$|-sinα•|$\frac{1+cosα}{sinα}$|
=cosα•($\frac{1+sinα}{-cosα}$)-sinα•($\frac{1+cosα}{-sinα}$)=-1-sinα-(-1-cosα)=cosα-sinα,
故选:A.
点评 本题主要考查三角函数的恒等变换,三角函数在各个象限中的符号,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
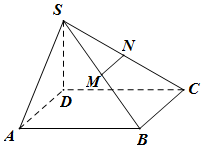 已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
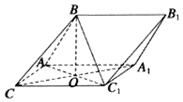 如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.
如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{3}$个单位长度 | B. | 向左平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{2π}{3}$个单位长度 | D. | 向左平移$\frac{2π}{3}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com