
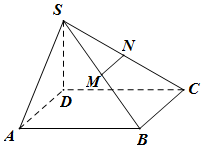
 已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.分析 (Ⅰ)取DC中点P,AB中点Q,连MQ、PQ、NP,则作出平面MNPQ,使面MNPQ∥面SAD.
(Ⅱ)由余弦定理求得$BD=2\sqrt{3}$,从而AD⊥BD,以D为原点,直线DA为x轴,直线DB为y轴,直线DS为z轴建立空间直角坐标系,利用向量法能求出二面角M-PQ-B的大小.
解答 解:(Ⅰ)如图,P是DC的中点,Q是AB的中点,
取DC中点P,AB中点Q,连MQ、PQ、NP,则作出平面MNPQ,使面MNPQ∥面SAD.
(若NP.PQ未作成虚线,扣两分)…(4分)
(Ⅱ)在平行四边形ABCD中,设AB=2AD=4,∠DCB=60°,
所以由余弦定理得$BD=2\sqrt{3}$,有AB2=AD2+BD2,所以AD⊥BD,….(5分)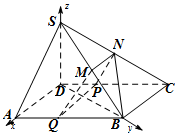 以D为原点,直线DA为x轴,直线DB为y轴,直线DS为z轴建立空间直角坐标系,
以D为原点,直线DA为x轴,直线DB为y轴,直线DS为z轴建立空间直角坐标系,
且$A({1,0,0}),B({0,\sqrt{3},0}),S({0,0,1}),M({0,\frac{{\sqrt{3}}}{2},\frac{1}{2}})$,
又$\overrightarrow{AQ}=\frac{1}{3}\overrightarrow{AB}$,设Q(x,y,z),则$Q({\frac{2}{3},\frac{{\sqrt{3}}}{3},0})$…(7分)
设平面的法向量为$\overrightarrow n=({x,y,z})$
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{AD}=0}\\{\overrightarrow n•\overrightarrow{MQ}=0}\end{array}}\right.$得$\overrightarrow n=({0,-\sqrt{3},1})$,…(9分)
易知面ABCD的法向量为$\overrightarrow m=({0,0,1})$
则$cos\left?{\vec m,\left.{\vec n}\right>}\right.=\frac{{|{\overrightarrow m\overrightarrow{•n}}|}}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{1}{2}$
所以二面角M-PQ-B为60°…(12分)
点评 本题考查满足条件的平面的作法,考查二面角的大小的求法,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x>0,则x>sinx恒成立 | |
| B. | 命题“若x-sinx=0,则x=0”的否命题为“若x-sinx≠0,则x≠0” | |
| C. | “命题p∧q为真”是“命题p∨q为真”的充分不必要条件 | |
| D. | 命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0<0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosα-sinα | B. | sinα+cosα+2 | C. | sinα-cosα | D. | -sinα-cosα-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com