
分析 (Ⅰ)求出函数的导数,根据函数的单调性求出f(x)的最大值,得到关于m的方程,求出m的值即可;
(Ⅱ)令F(x)=f(x)-g(x),求出函数的导数,通过讨论a的范围,得到函数的单调区间,结合函数恒成立问题,求出a的范围即可.
解答 解:(Ⅰ)函数f(x)的定义域为(-1,+∞),
f′(x)=1-m[ln(x+1)+1](1分)
因为m>0,所以f′(x)在(-1,+∞)上单调递减.
令f′(x)=0,得$x={e^{\frac{1}{m}-1}}-1$
当$x∈(-1,{e^{\frac{1}{m}-1}}-1)$时,f′(x)>0,f(x)单调递增;
当$x∈({e^{\frac{1}{m}-1}}-1,+∞)$时,f′(x)<0,f(x)单调递减;
所以,当$x={e^{\frac{1}{m}-1}}-1$时,$f{(x)_{max}}=f({e^{\frac{1}{m}-1}}-1)={e^{\frac{1}{m}-1}}-1-m{e^{\frac{1}{m}-1}}(\frac{1}{m}-1)$=$m{e^{\frac{1}{m}-1}}-1$
于是,$m{e^{\frac{1}{m}-1}}-1=0$,得${e^{\frac{1}{m}-1}}=\frac{1}{m}$(3分)
易知,函数y=ex-1-x在x=1处有唯一零点,所以$\frac{1}{m}=1$,m=1. (4分)
(Ⅱ)令F(x)=f(x)-g(x)=a(x2+2x)-(x+1)ln(x+1),x≥0
则F′(x)=a(2x+2)-[ln(x+1)+1](5分)
设h(x)=F′(x)=a(2x+2)-[ln(x+1)+1]
则${h^'}(x)=2a-\frac{1}{x+1}=\frac{2ax+2a-1}{x+1}$(6分)
①当a≤0时,h′(x)<0,F′(x)在[0,+∞)上单调递减,
则x∈[0,+∞)时,F′(x)≤F′(0)=2a-1<0,F(x)在[0,+∞)上单调递减,
故当x∈[0,+∞)时,F(x)≤F(0)=0,与已知矛盾.(8分)
②当$0<a<\frac{1}{2}$时,${h^'}(x)=2a-\frac{1}{x+1}=\frac{2ax+2a-1}{x+1}=\frac{{2a[x-(\frac{1}{2a}-1)]}}{x+1}$,
当$x∈(0,\frac{1}{2a}-1)$时,h′(x)<0,F′(x)在$(0,\frac{1}{2a}-1)$上单调递减,
则$x∈(0,\frac{1}{2a}-1)$时,F′(x)<F′(0)=2a-1<0
故F(x)在$(0,\frac{1}{2a}-1)$上单调递减,
则当$x∈(0,\frac{1}{2a}-1)$时,F(x)<F(0)=0,与已知矛盾.(10分)
③当$a≥\frac{1}{2}$时,h′(x)>0,F′(x)在[0,+∞)上单调递增,
则x∈[0,+∞)时,F′(x)≥F′(0)=2a-1>0
所以F(x)在[0,+∞)上单调递增,
故当x∈[0,+∞)时,F(x)≥F(0)=0恒成立.
综上,实数a的取值范围是$a≥\frac{1}{2}$. (12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
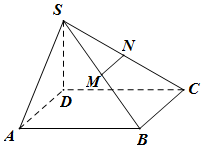 已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
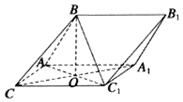 如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.
如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | (0,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com