
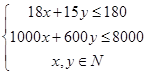
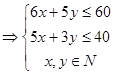
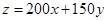
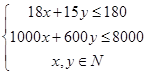
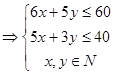 .........3分
.........3分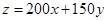 ............6分
............6分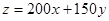 化为
化为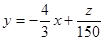
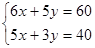 得
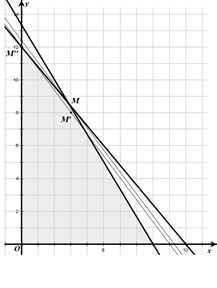
得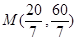 ,
,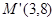 和
和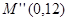 时z最大.........13分
时z最大.........13分

科目:高中数学 来源:不详 题型:填空题
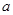
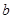 不小于6米,则菱形喷水池的两条对角线的长度之和
不小于6米,则菱形喷水池的两条对角线的长度之和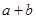 的
的查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
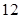 人
人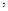 需配置两种型号的机器
需配置两种型号的机器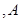 型机器需
型机器需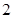 人操作
人操作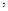 每天耗电
每天耗电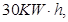 能生产出价值
能生产出价值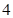 万元的产品
万元的产品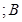 型机器需
型机器需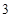 人操作
人操作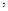 每天耗电
每天耗电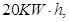 能生产出价值
能生产出价值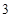 万元的产品现每天供应车间的电能不多于
万元的产品现每天供应车间的电能不多于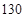
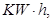 问该车间小组应如何配置两种型号的机器
问该车间小组应如何配置两种型号的机器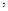 才能使每天的产值最大
才能使每天的产值最大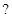 最大值是多少
最大值是多少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com