Question

11．已知点A（a，b）和点B（1，0）在直线3x-4y+10=0两侧，给出下列说法：
①3a-4b+10＞0；
②当a＞0时，a+b有最小值，无最大值；
③$\sqrt{{a^2}+{b^2}}＞2$；
④当a＞0且a≠1，b＞0时，$\frac{b}{a-1}$的取值范围为$（-∞，-\frac{5}{2}）∪（\frac{3}{4}，+∞）$．
其中所有正确说法的序号是（　　）

• A． ①②
• B． ②③
• C． ②③④
• D． ③④

Answer 1

分析 根据点A（a，b）与点B（1，0）在直线3x-4y+10=0的两侧，可以画出点A（a，b）所在的平面区域，进而结合二元一次不等式的几何意义，两点之间距离公式的几何意义，及两点之间连线斜率的几何意义，逐一分析四个答案．可得结论．

解答 解：∵点A（a，b）与点B（1，0）在直线3x-4y+10=0的两侧，
故点A（a，b）在如图所示的平面区域内，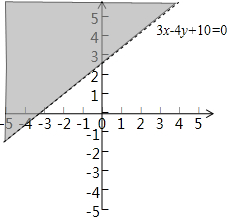

故3a-4b+10＜0，即①错误；
当a＞0时，a+b＞$\frac{5}{2}$，a+b无最小值，也无最大值，故②错误；
设原点到直线3x-4y+10=0的距离为d，则d=$\frac{10}{\sqrt{{3}^{2}+（-4）^{2}}}$=2，则$\sqrt{{a^2}+{b^2}}＞2$，故③正确；
当a＞0且a≠1，b＞0时，$\frac{b}{a-1}$表示点A（a，b）与B（1，0）连线的斜率，
∵当a=0，b=$\frac{5}{2}$时，$\frac{b}{a-1}$=-$\frac{5}{2}$，
又∵直线3x-4y+10=0的斜率为$\frac{3}{4}$，
故$\frac{b}{a-1}$的取值范围为（-∞，-$\frac{5}{2}$）∪（$\frac{3}{4}$，+∞），故④正确；
故选：D

点评 本题以命题的真假判断与应用为载体，考查了复合命题，指数函数的图象和性质，方程根的存在性与个数判断等知识点，难度中档．