Question

5．如图，将一个边长为1的正三角形的每条边三等分，以中间一段为边向形外作正三角形，并擦去中间一段，得图（2）．如此继续下去，得图（3）…，记第n个图形的边长a_n、周长为b_n．

（Ⅰ）求数列{a_n}、{b_n}的通项公式；
（Ⅱ）若第n个图形的面积为S_n，试探求S_n，S_n-1，（n≥2）满足的关系式，并证明S_n＜$\frac{2\sqrt{3}}{5}$．

Answer 1

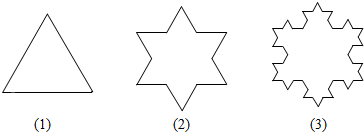
分析 （1）根据图形关系，建立图形边长和周长之间的关系即可求出数列的通项公式．
（2）根据归纳推理，求出两个图形的面积之间的关系，结合等比数列的通项公式进行求和即可得到结论．

解答 解：（Ⅰ）由题意知，从第2个图形起，每一个图形的边长均为上一个图形边长的$\frac{1}{3}$所以数列{a_n}是首项为1，公比为$\frac{1}{3}$的等比数列，则a_n=（$\frac{1}{3}$）^n-1，
设第n个图形的边数为c_n，因为第1个图形的边数为3，从第2个图形起，每一个图形的边数均为上一个图形边数的4倍，则c_n=3×4^n-1，
因此，第n个图形的周长b_n=a_n×c_n=（$\frac{1}{3}$）^n-1×3×4^n-1=3×（$\frac{4}{3}$）^n-1，
（Ⅱ）S₁=$\frac{\sqrt{3}}{4}$，当n≥2时，S_n=S_n-1+c_n×（$\frac{\sqrt{3}}{4}$×a_n²）=S_n-1+3×4^n-2×$\frac{\sqrt{3}}{4}$×[（$\frac{1}{3}$）^n-1]²=S_n-1+$\frac{3\sqrt{3}}{16}$×（$\frac{4}{9}$）^n-1，
则S_n=S₁+（S₂-S₁）+（S₃-S₂）+…+（S_n-S_n-1），
=$\frac{\sqrt{3}}{4}$+$\frac{3\sqrt{3}}{16}$[$\frac{4}{9}$+（$\frac{4}{9}$）²+（$\frac{4}{9}$）³+…++（$\frac{4}{9}$）^n-1]，
=$\frac{\sqrt{3}}{4}$+$\frac{3\sqrt{3}}{16}$×$\frac{\frac{4}{9}[1-（\frac{4}{9}）^{n-1}]}{1-\frac{4}{9}}$，
=$\frac{2\sqrt{3}}{5}$-$\frac{3\sqrt{3}}{20}$×（$\frac{4}{9}$）^n-1，
∴S_n＜$\frac{2\sqrt{3}}{5}$．

点评 本题主要考查数列通项公式和前n项和公式的应用，根据归纳推理建立数列的递推关系是解决本题的关键．综合性较强，属于中档题．