Question

16．2014 年12 月28 日开始，北京市公共电汽车和地铁按照里程分段计价．具体如下表．（不考虑公交卡折扣情况）

乘公共汽车方案	10公里（含）内2元； 10公里以上部分，每增加1元可乘坐5公里（含）
乘坐地铁方案（不含机场线）	6公里（含）内3元 6公里至12公里（含）4元 12公里至22公里（含）5元
	22公里至32公里（含）6元 32公里以上部分，每增加1元可乘坐20公里（含）

已知在北京地铁四号线上，任意一站到陶然亭站的票价不超过5 元，现从那些只乘坐四号线地铁，且在陶然亭出站的乘客中随机选出120 人，他们乘坐地铁的票价统计如图所示．
（Ⅰ）如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1 人，试估计此人乘坐地铁的票价小于5 元的概率；
（Ⅱ）从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选2 人，记x 为这2人乘坐地铁的票价和，根据统计图，并以频率作为概率，求X 的分布列和数学期望；
（Ⅲ）小李乘坐地铁从A 地到陶然亭的票价是5 元，返程时，小李乘坐某路公共电汽车所花交通费也是5 元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为s 公里，试写出s 的取值范围．（只需写出结论）

Answer 1

分析 （Ⅰ）根据统计图求出对应的人数和频率即可得到结论．
（Ⅱ）求出随机变量以及对应的概率，即可得到结论．
（Ⅲ）根据条件直接写出结论．

解答 解：（Ⅰ）设事件A：“此人乘坐地铁的票价小于5 元”，
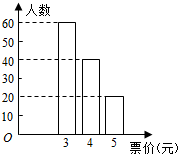
由统计图可知，得120人中票价为3元，4元，5元的人数分别为60，40，20人，
所以票价小于5的有60+40=100人，
故此人乘坐地铁的票价小于5 元的频率为$\frac{100}{120}$=$\frac{5}{6}$
则乘坐地铁的票价小于5 元的概率P（A）=$\frac{5}{6}$；
（Ⅱ）X的可能值为6，7，8，9，10．
统计图可知，得120人中票价为3元，4元，5元的频率分别为$\frac{60}{120}$=$\frac{1}{2}$，$\frac{40}{120}$=$\frac{1}{3}$，$\frac{20}{120}$=$\frac{1}{6}$，
以频率当概率，
则P（X=6）=$\frac{1}{2}×\frac{1}{2}$=$\frac{1}{4}$，P（X=7）=$\frac{1}{2}×\frac{1}{3}+\frac{1}{3}×\frac{1}{2}=\frac{1}{3}$，
P（X=8）=$\frac{1}{2}×\frac{1}{6}+\frac{1}{6}×\frac{1}{2}+\frac{1}{3}×\frac{1}{3}$=$\frac{5}{18}$，
P（X=9）=$\frac{1}{3}×\frac{1}{6}+\frac{1}{6}×\frac{1}{3}$=$\frac{1}{9}$，
P（X=10）=$\frac{1}{6}×\frac{1}{6}$=$\frac{1}{36}$，
则X的分布列为：

X	6	7	8	9	10
P	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{5}{18}$	$\frac{1}{9}$	$\frac{1}{36}$

则EX=6×$\frac{1}{4}$+7×$\frac{1}{3}+8×\frac{5}{18}+9×\frac{1}{9}$$+10×\frac{1}{36}$=$\frac{22}{3}$．
（Ⅲ）s∈（20，22]．

点评 本题主要考查概率和统计的综合应用，以及离散型随机变量的分布列和期望，考查学生的运算能力．