
分析 (1)由椭圆的标准方程可以求出椭圆的长轴长,短轴长,顶点,离心率
(2)由椭圆的定义可得|PF1|+|PF2|=2a,再由余弦定理可得|PF1|2+|PF2|2-|F1F2|2=2|PF1||PF2|cosθ,从而可得|PF1||PF2|=$\frac{2{b}^{2}}{1+cosθ}$,从而求△F1PF2的面积.
解答 解:(1)由椭圆$\frac{x^2}{25}$+$\frac{y^2}{9}$=1,可得a2=25,b2=9,c2=a2-b2=25-9=16,即a=5,b=3,c=4,
则长轴长为2a=10,短轴长2b=6,顶点分别为(5,0),(-5,0),(0,3),(0,-3),
e=$\frac{c}{a}$=$\frac{4}{5}$
(2)由题意,|PF1|+|PF2|=2a=10,
又∵|PF1|2+|PF2|2-|F1F2|2=2|PF1||PF2|cosθ,
∴(|PF1|+|PF2|)2-|F1F2|2=2|PF1||PF2|+2|PF1||PF2|cosθ,
∴4a2-4c2=2|PF1||PF2|(1+cosθ)=4b2=36,
∴|PF1||PF2|=$\frac{18}{1+coθ}$,
∴S△F1PF2=$\frac{1}{2}$|PF1||PF2|•sinθ=9•$\frac{sinθ}{1+cosθ}$=9tan$\frac{θ}{2}$.
点评 本题考查了椭圆的定义及余弦定理的应用,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,5} | B. | {1,3,4} | C. | {1,2,4} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(g(a-1))>f(g(a)) | B. | f(g($\frac{2a}{3}$))>f(g($\frac{5a}{3}$)) | ||
| C. | g(f($\frac{{4}^{n}+1}{{4}^{n}-1}$))>g(f(3))(其中a≠0且a$≠\frac{1}{2}$) | D. | g(f($\frac{{2}^{n}+1}{{2}^{n}-1}$))>g(f(3))(其中a≠0,且a≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
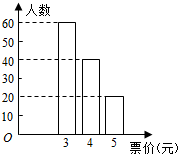 2014 年12 月28 日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)
2014 年12 月28 日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)| 乘公共汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含) |
| 乘坐地铁方案(不含机场线) | 6公里(含)内3元 6公里至12公里(含)4元 12公里至22公里(含)5元 |
| 22公里至32公里(含)6元 32公里以上部分,每增加1元可乘坐20公里(含) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1,p3 | B. | p1,p4 | C. | p2,p3 | D. | p2,p4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com