
分析 根据[x]的定义,结合f(x)的解析式,利用当n≤x<n+1时,f(x)=x-n这一特征分别进行判断即可.
解答 解:①函数f(x)定义域为R,假设n≤x<n+1,则f(x)=x-n∈[0,1),即①正确;
②假设n≤x<n+1,n+1≤x<n+2(n∈Z),则f(x)=x-n,f(x+1)=x+1-n-1=x-n,即f(x)=f(x+1),②正确;
③方程f(x)=kx+k有三个不同的根,即函数f(x)的图象与直线y=kx+k有三个不同交点,结合图象可知,k的取值范围应为$(-1,-\frac{1}{2}]∪[\frac{1}{4},\frac{1}{3})$,即③错误;
④若n≤x1≤x2<n+1(n∈Z),则f(x1)=x1-n,f(x2)=x2-n,故f(x1)≤f(x2),④正确.
故答案为:①②④
点评 本题主要考查命题的真假判断,利用[x]的意义,利用当n≤x<n+1时,f(x)=x-n这一特征是解决本题的关键.综合性较强,有一定的难度.


科目:高中数学 来源: 题型:解答题
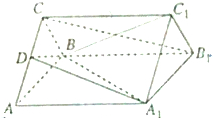 如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
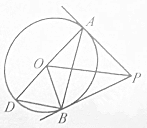 如图,点P在⊙O外,PA,PB切⊙O于A,B,AD为⊙O的直径,连结AB,OP,OB,BD,则图中与∠PAB相等的角有( )
如图,点P在⊙O外,PA,PB切⊙O于A,B,AD为⊙O的直径,连结AB,OP,OB,BD,则图中与∠PAB相等的角有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com