
分析 (Ⅰ)设出圆的一般方程,利用待定系数法求圆C的方程;
(Ⅱ)求出|AB|,P到AB距离的最大值为d+r,即可求△PAB的面积的最大值
解答 解:(Ⅰ)设所求圆的方程为x2+y2+Dx+Ey+F=0,
依题意得;$\left\{\begin{array}{l}1-E+F=0\\ 25+4D+3E+F=0\\ 3(-\frac{D}{2})-(-\frac{E}{2})-15=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}D=-12\\ E=6\\ F=5\end{array}\right.$,
∴所求圆的方程是x2+y2-12x+6y+5=0,
(Ⅱ)∵|AB|=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
由已知知直线AB的方程为x-y-1=0,
所以圆心C(6,-3)到AB的距离为d=4$\sqrt{2}$,…(9分)
P到AB距离的最大值为d+r=4$\sqrt{2}$+2$\sqrt{10}$,…(11分)
所以△PAB面积的最大值为$\frac{1}{2}$×$4\sqrt{2}$×(4$\sqrt{2}$+2$\sqrt{10}$)=$16+8\sqrt{5}$…(12分)
点评 本题考查圆的方程,考查三角形面积的计算,考查系数分析解决问题的能力,难度中档.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
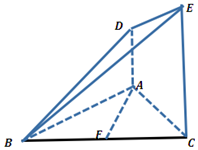 如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,
如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {2,3} | C. | {1,2,3} | D. | {2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-1,+∞) | C. | (-1,2] | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{6}$]与[$\frac{π}{2}$,$\frac{2π}{3}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [0,$\frac{π}{6}$]与[$\frac{2π}{3}$,π] | D. | [0,$\frac{π}{6}$]与[$\frac{π}{3}$,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
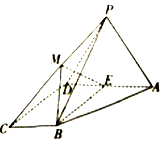 如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).
如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com