
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据∠BFD,|BF|=|FD|,推断出∠FBD=∠FBD=30°,进而表示出|FR|,|BF|,|BR|,|DF|,|DR|,进而表示出|BD|及圆的半径,进而利用抛物线的定义求得A到直线l的距离,利用三角形的面积,求得p的值.
解答 解:∵∠BFD=120°,|BF|=|FD|,
∴∠FBD=∠FBD=30°,
∵在Rt△BFR中,|FR|=p,
∴|BF|=2p,|BR|=$\sqrt{3}$p,
同理得:|DF|=2p,|DR|=$\sqrt{3}$p,
∴|BD|=|BR|+|RD|=2$\sqrt{3}$P,
圆F的半径|FA|=|FB|=2p,
由抛物线的定义可知A到l的距离d=|FA|=2p,
∵△ABD的面积为4$\sqrt{3}$,
∴$\frac{1}{2}$|BD|•d=4$\sqrt{3}$,即$\frac{1}{2}$•2$\sqrt{3}$p•2p=4$\sqrt{3}$,解得:p=$\sqrt{2}$或p=-$\sqrt{2}$(舍去),
p的值为$\sqrt{2}$,
故选B.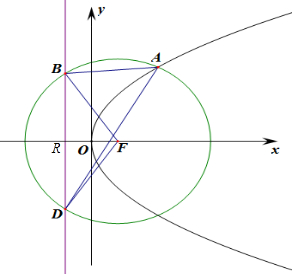
点评 本题主要考查了抛物线的基本性质,圆锥曲线的位置关系,圆的方程等问题.综合性强,计算量大,考查了学生分析推理和运算的能力,属于中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a⊥α,b∥β,α⊥β | B. | a?α,b⊥β,α∥β | C. | a⊥α,b⊥β,α∥β | D. | a?α,b∥β,α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,+∞) | C. | (-1,1)∪(1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [1,+∞) | C. | (-∞,5] | D. | [5,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com