
分析 (1)利用诱导公式,特殊角的三角函数值即可计算求值得解;
(2)利用诱导公式化简即可得解.
解答 解:(1)原式=$\frac{\sqrt{3}sin(-120°-3×360°)}{tan(3π+\frac{2π}{3})}$-cos(225°+360°)•tan(-9π-$\frac{1}{4}$π)
=$\frac{-\sqrt{3}sin120°}{tan\frac{2π}{3}}$+cos 225°tan$\frac{π}{4}$=$\frac{-\sqrt{3}sin60°}{-tan\frac{π}{3}}$+(-cos 45°)•tan$\frac{π}{4}$
=$\frac{\sqrt{3}•\frac{\sqrt{3}}{2}}{\sqrt{3}}$+(-$\frac{\sqrt{2}}{2}$)×1=$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}$.
(2)原式=$\frac{sinα}{cosα}$•sinα•cosα=sin2α.
点评 本题主要考查了诱导公式,特殊角的三角函数值在三角函数化简求值中的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | -1,4 | B. | 3,$\frac{1}{2}$ | C. | $\frac{1}{2},-\frac{5}{4}$ | D. | 3,$-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x0)<0 | B. | f′(x0)>0 | C. | f′(x0)=0 | D. | f′(x0)不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=2n-3 | B. | an=2n-4 | C. | an=3-3n | D. | an=2n-5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{6}$,$\frac{1}{4}$) | B. | ($\frac{1}{6}$,$\frac{1}{2e}$) | C. | ($\frac{1}{8}$,$\frac{1}{2e}$) | D. | ($\frac{1}{2e}$,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
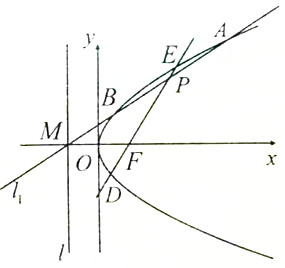 已知抛物线C:y2=2px(p>0)的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合,抛物线C的准线l与x轴的交点为M,过点M且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF与抛物线C交于D,E两点
已知抛物线C:y2=2px(p>0)的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合,抛物线C的准线l与x轴的交点为M,过点M且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF与抛物线C交于D,E两点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com