
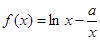 ,
,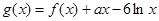 ,其中
,其中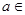 R.
R.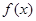 的单调性;
的单调性;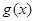 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数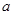 的取值范围;
的取值范围;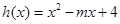 ,当
,当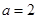 时,若
时,若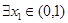 ,
,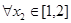 ,总有
,总有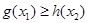 成立,求实数
成立,求实数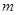 的取值范围.
的取值范围.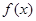 在
在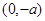 上单调递减,在
上单调递减,在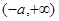 上单调递增;(2)
上单调递增;(2)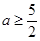 ;(3)
;(3)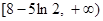 .
.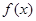 求导,由于
求导,由于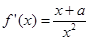 的正负与参数
的正负与参数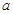 有关,故要对
有关,故要对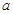 分类讨论来研究单调性; (2)先由
分类讨论来研究单调性; (2)先由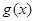 在其定义域内为增函数转化为在不等式
在其定义域内为增函数转化为在不等式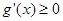 中求参数范围的问题,利用分离参数法和基本不等式的知识求出参数
中求参数范围的问题,利用分离参数法和基本不等式的知识求出参数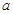 的取值范围;(3)先通过导数研究
的取值范围;(3)先通过导数研究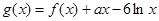 在
在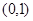 的最值,然后根据命题“若
的最值,然后根据命题“若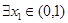 ,
,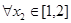 ,总有
,总有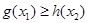 成立”分析得到
成立”分析得到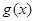 在
在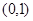 上的最大值不小于
上的最大值不小于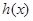 在
在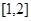 上的最大值,从而列出不等式组求出参数
上的最大值,从而列出不等式组求出参数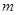 的取值范围.
的取值范围.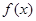 的定义域为
的定义域为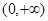 ,且
,且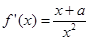 , 1分
, 1分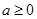 时,
时,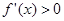 ,
,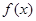 在
在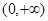 上单调递增; 2分
上单调递增; 2分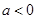 时,由
时,由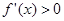 ,得
,得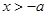 ;由
;由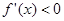 ,得
,得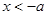 ;
;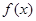 在
在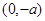 上单调递减,在
上单调递减,在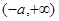 上单调递增. 4分
上单调递增. 4分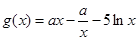 ,
,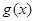 的定义域为
的定义域为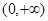
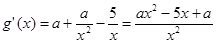 5分
5分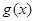 在其定义域内为增函数,所以
在其定义域内为增函数,所以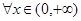 ,
,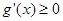
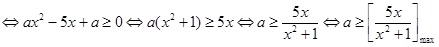
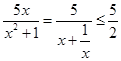 ,当且仅当
,当且仅当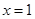 时取等号,所以
时取等号,所以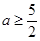 8分
8分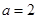 时,
时,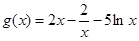 ,
,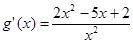
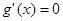 得
得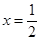 或
或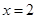
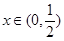 时,
时,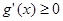 ;当
;当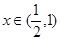 时,
时,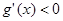 .
.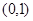 上,
上,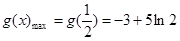 10分
10分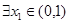 ,
,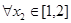 ,总有
,总有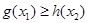 成立”等价于
成立”等价于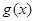 在
在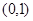 上的最大值不小于
上的最大值不小于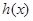 在
在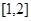 上的最大值”
上的最大值”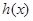 在
在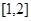 上的最大值为
上的最大值为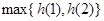
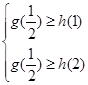 12分
12分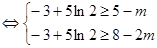
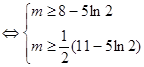
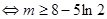
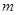 的取值范围是
的取值范围是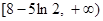 14分
14分

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com