
分析 设对称点的坐标为Q(x,y,z),利用中点公式求得x、y、z的值,可得结论.
解答 解:设点P(-1,6,-3)关于点M(2,4,5)的对称点的坐标为Q(x,y,z),
则由M为线段PQ的中点,可得$\left\{\begin{array}{l}{2=\frac{-1+x}{2}}\\{4=\frac{6+y}{2}}\\{5=\frac{-3+z}{2}}\end{array}\right.$,求得$\left\{\begin{array}{l}{x=5}\\{y=2}\\{z=13}\end{array}\right.$,
故对称点的坐标为Q(5,2,13),
故答案为:(5,2,13).
点评 本题主要考查求一个点关于另一个点的对称点的坐标的方法,利用了中点公式,属于基础题.


科目:高中数学 来源: 题型:解答题
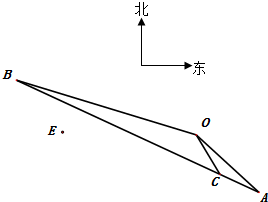 如图,某自行车手从O点出发,沿折线O-A-B-O匀速骑行,其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°-α)(其中sinα=$\frac{1}{{\sqrt{26}}}$,0°<α<90°)且与点O相距5$\sqrt{13}$千米(假设所有路面及观测点都在同一水平面上).
如图,某自行车手从O点出发,沿折线O-A-B-O匀速骑行,其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°-α)(其中sinα=$\frac{1}{{\sqrt{26}}}$,0°<α<90°)且与点O相距5$\sqrt{13}$千米(假设所有路面及观测点都在同一水平面上).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=($\sqrt{x}$)2与y=x | B. | y=$\sqrt{{x}^{2}}$与 y=($\sqrt{x}$)2 | C. | y=$\root{3}{{x}^{3}}$与y=$\frac{{x}^{2}}{x}$ | D. | y=($\root{3}{{x}^{3}}$)3与y=x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
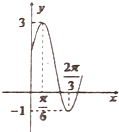 如图所示,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象的一部分,则函数解析式是( )
如图所示,是函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象的一部分,则函数解析式是( )| A. | $y=2sin(2x+\frac{π}{6})+1$ | B. | $y=sin(2x+\frac{π}{3})+1$ | C. | $y=2sin(\frac{1}{2}x+\frac{π}{6})+2$ | D. | $y=sin(2x+\frac{π}{3})+2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com