Question

2．如图，在三棱锥A-BCD中，△ACD与△BCD都是边长为2的正三角形，且平面ACD⊥平面BCD，则该三棱锥外接球的表面积为$\frac{20}{3}π$．

Answer 1

分析 取AB，CD中点分别为E，F，连接EF，AF，BF，求出EF，判断三棱锥的外接球球心O在线段EF上，连接OA，OC，求出半径，然后求解表面积．

解答 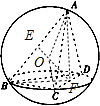解：取AB，CD中点分别为E，F，连接EF，AF，BF，由题意知AF⊥BF，AF=BF，$EF=\frac{{\sqrt{6}}}{2}$，易知三棱锥的外接球球心O在线段EF上，
连接OA，OC，有R²=AE²+OE²，R²=CF²+OF²，
求得${R^2}=\frac{5}{3}$，所以其表面积为$\frac{20}{3}π$．
故答案为：$\frac{20}{3}π$．

点评 本小题主要考查球的内接几何体的相关计算问题，对考生的空间想象能力与运算求解能力以及数形结合思想都提出很高要求，本题是一道综合题，属于较难题．