
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心为原点,焦点
的中心为原点,焦点![]() ,
,![]() 在
在![]() 轴上,离心率为
轴上,离心率为![]() .过
.过![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆![]() 与
与![]() 轴正半轴相交于两点
轴正半轴相交于两点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),过点
的左侧),过点![]() 任作一条直线与椭圆
任作一条直线与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,连接
两点,连接![]() ,
,![]() ,求证
,求证![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)设椭圆C的方程为![]() (a>b>0),由离心率为
(a>b>0),由离心率为![]() ,得
,得![]() ,又△PQF2的周长为4a=
,又△PQF2的周长为4a=![]() ,得a=2
,得a=2![]() ,进而求出椭圆方程;
,进而求出椭圆方程;
(2)把y=0代入圆的方程求出x的值,确定M与N的坐标,当AB⊥x轴时,由椭圆的对称性得证;当AB与x轴不垂直时,设直线AB为y=k(x﹣1),与椭圆方程联立得到关于x的一元二次方程,设A(x1,y1),B(x2,y2),利用韦达定理表示出x1+x2,x1x2,进而表示出直线AN与直线BN斜率之和为0,即可得证.
(1)设椭圆C的方程为![]() (a>b>0).因为离心率为
(a>b>0).因为离心率为![]() ,所以
,所以![]() ,解得
,解得![]() ,即
,即![]() .又△PQF2的周长为|PQ|+|PF2|+|QF2|=(|PF1|+|PF2|)+(|QF1|+|QF2|)=2a+2a=4a,所以又△PQF2的周长为,即a=2
.又△PQF2的周长为|PQ|+|PF2|+|QF2|=(|PF1|+|PF2|)+(|QF1|+|QF2|)=2a+2a=4a,所以又△PQF2的周长为,即a=2![]() ,b=2,
,b=2,
所以椭圆C的方程为![]() .
.
(2)把y=0代入![]() +(y-2)2=
+(y-2)2=![]() ,解得x=1或x=4,因为点
,解得x=1或x=4,因为点![]() 在点
在点![]() 的左侧,即点M(1,0),N(4,0).
的左侧,即点M(1,0),N(4,0).
①当AB⊥x轴时,由椭圆的对称性可知∠ANM=∠BNM.
②当AB与x轴不垂直时,可设直线AB的方程为y=k(x-1).
联立![]() (k2+2)x2-2k2x+k2-8=0.
(k2+2)x2-2k2x+k2-8=0.
设A(x1,y1),B(x2,y2),
则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
因为y1=k(x1-1),y2=k(x2-1),
所以kAN+kBN=![]() +
+![]() =
=![]() +
+![]() =
=![]() .
.
因为(x1-1)(x2-4)+(x2-1)(x1-4)=2x1x2-5(x1+x2)+8=![]() +8=
+8=![]() ,
,
所以kAN+kBN=0,所以∠ANM=∠BNM,综上所述,∠ANM=∠BNM.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数且
为参数且 ![]() )曲线
)曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的交点到极点的距离;
的交点到极点的距离;
(2)设![]() 与
与![]() 交于
交于![]() 点,
点,![]() 与
与![]() 交于
交于![]() 点,当
点,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有____________(把所有正确的序号都填上).
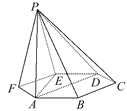
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来大气污染防治工作得到各级部门的重视,某企业在现有设备下每日生产总成本![]() (单位:万元)与日产量
(单位:万元)与日产量![]() (单位:吨)之间的函数关系式为
(单位:吨)之间的函数关系式为![]() ,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为
,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为![]() 万元,除尘后当日产量
万元,除尘后当日产量![]() 时,总成本
时,总成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每吨产品出厂价为48万元,试求除尘后日产量为多少时,每吨产品的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,两焦点分别为双曲线
的中心在坐标原点,两焦点分别为双曲线![]() 的顶点,直线
的顶点,直线![]() 与椭圆
与椭圆![]() 交于A,B两点,且点A的坐标为
交于A,B两点,且点A的坐标为![]() ,点Р是椭圆
,点Р是椭圆![]() 上异于A,B的任意一点,点Q满足
上异于A,B的任意一点,点Q满足![]() ,
,![]() ,且A,B,Q三点不共线.
,且A,B,Q三点不共线.
(1)求椭圆![]() 的方程;
的方程;
(2)求点Q的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com