
分析 (1)设出椭圆的焦点F(c,0),直线l:y=x-c,设M(x1,y1),N(x2,y2),代入椭圆方程,运用韦达定理,再由向量共线的坐标表示,化简整理,即可得到所求值;
(2)运用韦达定理和a,b,c的关系,以及直线的斜率公式,即可得到定值;
(3)设A(m,n),则有$\frac{{m}^{2}}{{a}^{2}}$+$\frac{{n}^{2}}{{b}^{2}}$=1,运用向量共线的坐标表示,两边平方,化简可得2α2+2β2=1,设α=$\frac{\sqrt{2}}{2}$cosθ,β=$\frac{\sqrt{2}}{2}$sinθ,0≤θ<2π,再由二倍角的正弦公式和正弦函数的值域,即可得到最大值.
解答 解:(1)椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F(c,0),
可得直线l:y=x-c,
设M(x1,y1),N(x2,y2),
联立椭圆方程,可得(b2+a2)x2-2ca2x+a2c2-a2b2=0,
即有x1+x2=$\frac{2c{a}^{2}}{{b}^{2}+{a}^{2}}$,y1+y2=x1+x2-2c=-$\frac{2c{b}^{2}}{{b}^{2}+{a}^{2}}$,
由$\overrightarrow{OM}$+$\overrightarrow{ON}$=λ(3,-1),可得(x1+x2,y1+y2)=(3λ,-λ),
即有a2=3b2,即为$\frac{a}{b}$=$\sqrt{3}$;
(2)证明:由(1)可得,x1+x2=$\frac{2c{a}^{2}}{{b}^{2}+{a}^{2}}$=$\frac{3c}{2}$,
x1x2=$\frac{{a}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$=$\frac{3}{4}$(c2-b2)=$\frac{3}{4}$(c2-$\frac{1}{2}$c2)=$\frac{3}{8}$c2,
则k1•k2=$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=$\frac{{x}_{1}-c}{{x}_{1}}$•$\frac{{x}_{2}-c}{{x}_{2}}$=$\frac{{x}_{1}{x}_{2}-c({x}_{1}+{x}_{2})+{c}^{2}}{{x}_{1}{x}_{2}}$
=$\frac{\frac{3}{8}{c}^{2}-c•\frac{3c}{2}+{c}^{2}}{\frac{3{c}^{2}}{8}}$=-$\frac{1}{3}$为定值;
(3)设A(m,n),则有$\frac{{m}^{2}}{{a}^{2}}$+$\frac{{n}^{2}}{{b}^{2}}$=1,
由$\overrightarrow{OA}$=α($\overrightarrow{OM}$+$\overrightarrow{ON}$)+β$\overrightarrow{MN}$=α($\overrightarrow{OM}$+$\overrightarrow{ON}$)+β($\overrightarrow{ON}$-$\overrightarrow{OM}$)
=(α-β)$\overrightarrow{OM}$+(α+β)$\overrightarrow{ON}$,
即有$\left\{\begin{array}{l}{m=(α-β){x}_{1}+(α+β){x}_{2}}\\{n=(α-β){y}_{1}+(α+β){y}_{2}}\end{array}\right.$,
由$\frac{{m}^{2}}{{a}^{2}}$+$\frac{{n}^{2}}{{b}^{2}}$=(α-β)2•($\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$)+(α+β)2•($\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$)+2(α2-β2)($\frac{{x}_{1}{x}_{2}}{{a}^{2}}$+$\frac{{y}_{1}{y}_{2}}{{b}^{2}}$)
=(α-β)2+(α+β)2+2(α2-β2)($\frac{{x}_{1}{x}_{2}}{{a}^{2}}$+$\frac{{y}_{1}{y}_{2}}{{b}^{2}}$)
=2α2+2β2+2(α2-β2)($\frac{{x}_{1}{x}_{2}}{{a}^{2}}$-$\frac{{x}_{1}{x}_{2}}{3{b}^{2}}$)=2α2+2β2=1,
设α=$\frac{\sqrt{2}}{2}$cosθ,β=$\frac{\sqrt{2}}{2}$sinθ,0≤θ<2π,
即有αβ=$\frac{1}{2}$cosθsinθ=$\frac{1}{4}$(2sinθcosθ)=$\frac{1}{4}$sin2θ≤$\frac{1}{4}$,
当2θ=$\frac{π}{2}$,即θ=$\frac{π}{4}$时,αβ取得最大值,且为$\frac{1}{4}$.
点评 本题考查椭圆的方程和运用,考查向量共线的坐标表示,以及直线方程和椭圆方程联立,运用韦达定理,同时考查换元法的运用和三角函数的恒等变换及正弦函数的值域的运用,属于中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
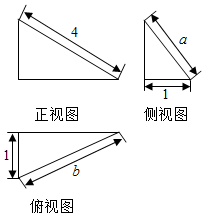
| A. | $\frac{4}{3}$ | B. | $\frac{8}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{16}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
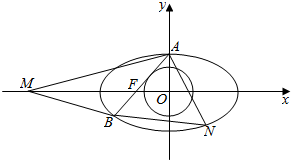 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
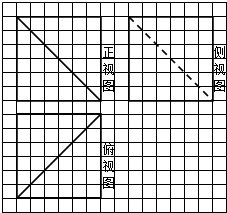 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截去部分的几何体的表面积为54+18$\sqrt{3}$.
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截去部分的几何体的表面积为54+18$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
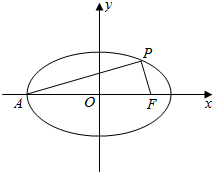 如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,右焦点为F(c,0),P(x0,y0)为椭圆上一点且PA⊥PF.
如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,右焦点为F(c,0),P(x0,y0)为椭圆上一点且PA⊥PF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com