Question

7．如图：三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，BC⊥AC，M是AB上的动点，CB=CA=CC₁=2．
（Ⅰ）若点M是AB中点，证明：平面MCC₁⊥平面ABB₁A₁；
（Ⅱ）判断点M到平面A₁B₁C的距离是否为定值？若是，求出定值；若不是，请说明理由．

Answer 1

分析 （Ⅰ）推导出CM⊥AB，CM⊥AA₁，从而CM⊥平面ABB₁A₁，由此能证明平面MCC₁⊥平面ABB₁A₁．
（Ⅱ）推导出AB∥平面A₁B₁C，从而点M到平面A₁B₁C的距离是定值，令点M平分AB，作A₁B₁的中点M₁，过M作MO⊥CM₁，垂足为O，推导出MO是点M到平面A₁B₁C的距离，由此能示出点M到平面A₁B₁C的距离．

解答 证明：（Ⅰ）∵BC=AC，M是AB中点，∴CM⊥AB，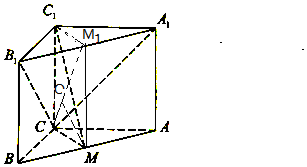
∵AA₁⊥平面ABC，CM?平面图ABC，∴CM⊥AA₁，
∵AB?平面ABB₁A₁，AA₁?平面ABB₁A₁，且AB∩AA₁=A，
∴CM⊥平面ABB₁A₁，
∵CM?平面MCC₁，
∴平面MCC₁⊥平面ABB₁A₁．
解：（Ⅱ）∵AB∥A₁B₁，A₁B₁?平面A₁B₁C，AB?平面A₁B₁C，
∴AB∥平面A₁B₁C，
∴点M到平面A₁B₁C的距离是定值，
令点M平分AB，作A₁B₁的中点M₁，
连结MM₁，C₁M₁，CM₁，
过M作MO⊥CM₁，垂足为O，
由题意知C、M、M₁、C₁共面，
∵AB⊥平面MCC₁M₁，AB∥A₁B₁，
∴A₁B₁⊥平面MCC₁M₁，
∵MO?平面MCC₁M₁，∴A₁B₁⊥MO，
又∵MO⊥CM₁，CM₁?平面A₁B₁C，A₁B₁?平面A₁B₁C，
∴MO⊥平面A₁B₁C，即MO是点M到平面A₁B₁C的距离，
∵CB=CA=CC₁=2，BC⊥AC，∴AB=$\sqrt{C{A}^{2}+C{B}^{2}}$=2$\sqrt{2}$，
∴CM=$\sqrt{B{C}^{2}-B{M}^{2}}$=$\sqrt{2}$，∴CM₁=$\sqrt{C{M}^{2}+M{{M}_{1}}^{2}}$=$\sqrt{6}$，
∵$\frac{1}{2}•MO•C{M}_{1}$=$\frac{1}{2}•CM•M{M}_{1}$，∴$\overrightarrow{MO}$=$\frac{\sqrt{2}•2}{\sqrt{6}}=\frac{2\sqrt{3}}{3}$，
∴点M到平面A₁B₁C的距离为定值$\frac{2\sqrt{3}}{3}$．

点评 本题考查面面垂直的证明，考查点到面的距离是否是定值的判断与求法，考查空间中线线、线面、面面的位置关系等基础知识，考查推理论证能力、数据处理能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．