
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值;
的值;
(2)设![]() ,试讨论函数
,试讨论函数![]() 的单调性;
的单调性;
(3)当![]() 时,若存在正实数
时,若存在正实数![]() 满足
满足![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() .(2)见解析(3)见解析
.(2)见解析(3)见解析
【解析】
(Ⅰ)由题意,求得函数的导数![]() ,根据
,根据![]() ,即可求解;
,即可求解;
(Ⅱ)由题意,得![]()
![]() ,求得函数的导数
,求得函数的导数![]() ,分类讨论,即可求解函数的单调区间;
,分类讨论,即可求解函数的单调区间;
(Ⅲ)代入![]() ,求出
,求出![]() ,令
,令![]() ,
,![]() ,根据函数的单调性,即可作出证明.
,根据函数的单调性,即可作出证明.
(1)因为![]() ,所以
,所以![]() ,
,
因为![]() 在
在![]() 处取得极值,
处取得极值,
所以![]() ,解得
,解得![]() .
.
验证:当![]() 时,
时,![]() 在
在![]() 处取得极大值.
处取得极大值.
(2)解:因为![]()
![]()
所以![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 函数
函数![]() 在
在![]() 上单调递减.
上单调递减.
②若![]() ,
,![]() ,
,
当![]() 时,易得函数
时,易得函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 恒成立,所以函数
恒成立,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,易得函数
时,易得函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减.
上单调递减.
(3)证明:当![]() 时,
时,![]() ,
,
因为![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]() .
.
令![]() ,
,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
所以函数![]() 在
在![]() 时,取得最小值,最小值为
时,取得最小值,最小值为![]() .
.
所以![]() ,
,
即![]() ,所以
,所以![]() 或
或![]() .
.
因为![]() 为正实数,所以
为正实数,所以![]() .
.
当![]() 时,
时,![]() ,此时不存在
,此时不存在![]() 满足条件,
满足条件,
所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知圆O:![]() 与直线
与直线![]() 相切.
相切.
(1)求圆O的方程;
(2)若过点![]() 的直线l被圆O所截得的弦长为4,求直线l的方程;
的直线l被圆O所截得的弦长为4,求直线l的方程;
(3)若过点![]() 作两条斜率分别为
作两条斜率分别为![]() ,
,![]() 的直线交圆O于B、C两点,且
的直线交圆O于B、C两点,且![]() ,求证:直线BC恒过定点.并求出该定点的坐标.
,求证:直线BC恒过定点.并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织了一次新高考质量测评,在成绩统计分析中,某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
5 | 6 | 8 | ||||||||
6 | 2 | 3 | 3 | 5 | 6 | 8 | 9 | |||
7 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
8 | ||||||||||
9 | 5 | 8 |

(1)求该班数学成绩在![]() 的频率及全班人数;
的频率及全班人数;
(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定90分及其以上为优秀,现从该班分数在80分及其以上的试卷中任取2份分析学生得分情况,求在抽取的2份试卷中至少有1份优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F为椭圆C的右焦点.A(-a,0),|AF|=3.
,F为椭圆C的右焦点.A(-a,0),|AF|=3.

(I)求椭圆C的方程;
(II)设O为原点,P为椭圆上一点,AP的中点为M.直线OM与直线x=4交于点D,过O且平行于AP的直线与直线x=4交于点E.求证:∠ODF=∠OEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学解答一道解析几何题:“已知直线l:![]() 与x轴的交点为A,圆O:
与x轴的交点为A,圆O:![]() 经过点A.
经过点A.
(Ⅰ)求r的值;
(Ⅱ)若点B为圆O上一点,且直线AB垂直于直线l,求![]() .”
.”
该同学解答过程如下:
解答:(Ⅰ)令![]() ,即
,即![]() ,解得
,解得![]() ,所以点A的坐标为
,所以点A的坐标为![]() .
.
因为圆O:![]() 经过点A,所以
经过点A,所以![]() .
.
(Ⅱ)因为![]() .所以直线AB的斜率为
.所以直线AB的斜率为![]() .
.
所以直线AB的方程为![]() ,即
,即![]() .
.
代入![]() 消去y整理得
消去y整理得![]() ,
,
解得![]() ,
,![]() .当
.当![]() 时,
时,![]() .所以点B的坐标为
.所以点B的坐标为![]() .
.
所以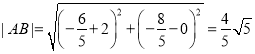 .
.
指出上述解答过程中的错误之处,并写出正确的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com