
分析 (1)利用绝对值的几何意义,化简函数的解析式,然后列出不等式求解即可.
(2)求出函数的值域,转化不等式,得到二次不等式,求解即可.
解答 解:(1)由f(x)=|2x+1|-|x-4|=$\left\{\begin{array}{l}{-x-5,x≤-\frac{1}{2}}\\{3x-3,-\frac{1}{2}<x<4}\\{x+5,x≥4}\end{array}\right.$
f(x)≥0,可得:$\left\{\begin{array}{l}{x≤-\frac{1}{2}}\\{-x-5≥0}\end{array}\right.$或$\left\{\begin{array}{l}{-\frac{1}{2}<x<4}\\{3x-3≥0}\end{array}\right.$或$\left\{\begin{array}{l}{x≥4}\\{x+5≥0}\end{array}\right.$…(2分)
解得:{x|x≤-5或x≥1};…(5分)
(2)当x0∈[-7,7],时,f(x0)∈[-$\frac{9}{2}$,12],…(7分)
由题意f(x0)+$\frac{1}{2}$m2<4m知,-$\frac{9}{2}$<4m-$\frac{1}{2}$m2,即m2-8m-9<0,
解得:-1<m<9…(10分)
点评 本题考查绝对值函数的应用,函数恒成立以及转化思想的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
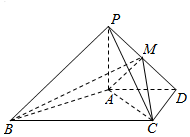 如图.在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ADC=90°,且PA=2,AD=CD=$\frac{1}{2}$BC=2$\sqrt{2}$,点M在PD上.
如图.在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ADC=90°,且PA=2,AD=CD=$\frac{1}{2}$BC=2$\sqrt{2}$,点M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 认为应该拆除 | 认为太可惜了 | 总计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 总计 | 75 | 25 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超过1%的前提下,认为“是否认为拆除太可惜了与性别有关” | |
| B. | 在犯错误的概率不超过1%的前提下,认为“是否认为拆除太可惜了与性别无关” | |
| C. | 有90%以上的把握认为“是否认为拆除太可惜了与性别有关” | |
| D. | 有90%以上的把握认为“是否认为拆除太可惜了与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 孵化鸭雏 | B. | 商品鸭饲养 | ||
| C. | 商品鸭收购、育肥、加工 | D. | 羽绒服加工生产体系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{2}$ | C. | $\frac{2}{π}$ | D. | -$\frac{2}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com