
分析 (1)f(x)=$\overrightarrow a$•$\overrightarrow b$=x2+cx,故f(1)=1+c=2,求出c值,可得函数f(x)的表达式;
(2)g(x)=f(x)-|λx-1|=$\left\{\begin{array}{l}{x}^{2}+(1+λ)x-1,x<\frac{1}{λ}\\{x}^{2}+(1-λ)x+1,x≥\frac{1}{λ}\end{array}\right.$,(λ>0).结合二次函数的图象和性质,可得函数g(x)的单调区间;
(3)函数g(x)在区间(0,1)上的零点个数即f(x)=x2+x和y=|λx-1|的图象交点的个数,数形结合,可得答案.
解答 解:(1)∵$\overrightarrow a$=(x2,c),$\overrightarrow b$=(1,x),
∴f(x)=$\overrightarrow a$•$\overrightarrow b$=x2+cx,
∵f(1)=1+c=2,
解得:c=1,
∴f(x)=x2+x,
(2)g(x)=f(x)-|λx-1|=$\left\{\begin{array}{l}{x}^{2}+(1+λ)x-1,x<\frac{1}{λ}\\{x}^{2}+(1-λ)x+1,x≥\frac{1}{λ}\end{array}\right.$,(λ>0).
当λ≤2时,函数g(x)的单调递减区间为(-∞,$-\frac{1+λ}{2}$],单调递增区间为[$-\frac{1+λ}{2}$,+∞);
当λ>2时,函数g(x)的单调递减区间为(-∞,$-\frac{1+λ}{2}$],[$\frac{1}{λ}$,$\frac{λ-1}{2}$],单调递增区间为[$-\frac{1+λ}{2}$,$\frac{1}{λ}$],[$\frac{λ-1}{2}$,+∞);
(3)令g(x)=f(x)-|λx-1|=0,
则f(x)=|λx-1|,
在同一坐标系中画出f(x)=x2+x和y=|λx-1|的图象如下图所示: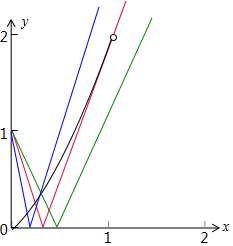
当λ=3时,y=3x-1与y=x2+x切于(1,2)点,
故由图可得:λ>3时,f(x)=x2+x和y=|λx-1|的图象在区间(0,1)上有两个交点,
即函数g(x)在区间(0,1)上有两个零点
0<λ≤3时,f(x)=x2+x和y=|λx-1|的图象在区间(0,1)上有一个交点,
即函数g(x)在区间(0,1)上有一个零点.
点评 本题考查的知识点是数形结合思想,分类讨论思想,转化思想,函数的零点个数及判断,向量的数量积,函数的单调性,难度中档.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
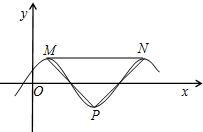 函数f(x)=$\frac{1}{2}$sin(ωx+$\frac{π}{6}$)(ω>0)的部分图象如图所示,设M,N是图象上的最高点,P是图象上的最低点,若△PMN为等腰直角三角形,则ω=( )
函数f(x)=$\frac{1}{2}$sin(ωx+$\frac{π}{6}$)(ω>0)的部分图象如图所示,设M,N是图象上的最高点,P是图象上的最低点,若△PMN为等腰直角三角形,则ω=( )| A. | 1 | B. | 2 | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
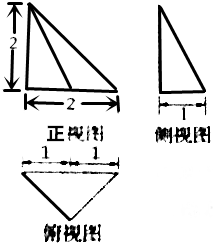
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 18种 | C. | 24种 | D. | 30种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
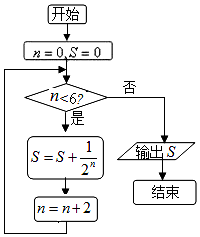
| A. | $\frac{5}{4}$ | B. | $\frac{21}{16}$ | C. | $\frac{63}{32}$ | D. | $\frac{85}{64}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com