
分析 化简参数方程为普通方程,求出F与l的方程,然后求解A的坐标,利用三角形的面积列出方程,求解即可.
解答 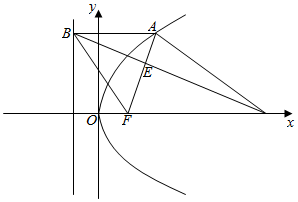 解:抛物线$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$(t为参数,p>0)的普通方程为:y2=2px焦点为F($\frac{p}{2}$,0),如图:过抛物线上一点A作l的垂线,垂足为B,设C($\frac{7}{2}$p,0),AF与BC相交于点E.|CF|=2|AF|,
解:抛物线$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$(t为参数,p>0)的普通方程为:y2=2px焦点为F($\frac{p}{2}$,0),如图:过抛物线上一点A作l的垂线,垂足为B,设C($\frac{7}{2}$p,0),AF与BC相交于点E.|CF|=2|AF|,
|CF|=3p,|AB|=|AF|=$\frac{3}{2}$p,A(p,$\sqrt{2}p$),
△ACE的面积为3$\sqrt{2}$,$\frac{AE}{EF}=\frac{AB}{CF}=\frac{1}{2}$,
可得$\frac{1}{3}{S}_{△AFC}$=S△ACE.
即:$\frac{1}{3}×\frac{1}{2}×3p×\sqrt{2}p$=3$\sqrt{2}$,
解得p=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查抛物线的简单性质的应用,抛物线的参数方程的应用,考查分析问题解决问题的能力.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
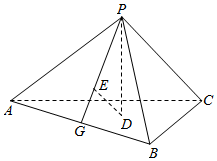 如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤a} | B. | {x|x>0或x<-$\frac{4}{5}$a} | ||
| C. | {x|-$\frac{a}{2}$<x<a} | D. | {x|-a≤x<-$\frac{4}{5}$a或0<x≤a} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com