
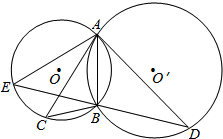
 如图,⊙O和⊙O′相交于A、B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB并延长交⊙O于点E.
如图,⊙O和⊙O′相交于A、B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB并延长交⊙O于点E.分析 (1)利用弦切角定理得出∠CAB=∠ADB,∠ACB=∠DAB,从而△ACB∽△DAB,即可证明结论;
(2)证明△EAD∽△ABD,可得AE•BD=AD•AB结合(1)的结论,AC=AE,即可得出结论.
解答 (1)证明:由AC与圆O′相切于点A,得∠CAB=∠ADB,
同理,∠ACB=∠DAB,
从而△ACB∽△DAB,
所以$\frac{AC}{AD}=\frac{AB}{BD}$,
所以AC•BD=AD•AB.
(2)解:由AD与⊙O相切于A,得∠AED=∠BDA,又∠ADE=∠BDA,
得△EAD∽△ABD,从而$\frac{AE}{AB}=\frac{AD}{BD}$=$\frac{DE}{AD}$,
即AE•BD=AD•AB
结合(1)的结论,AC=AE.
又AD=4,AC=2AB,所以DE=$\frac{1}{2}AD$=2.
点评 本题考查弦切角定理,考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
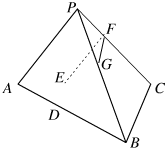 如图,平面α截三棱锥P-ABC得截面DEFG,设PA∥α,BC∥α.
如图,平面α截三棱锥P-ABC得截面DEFG,设PA∥α,BC∥α.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
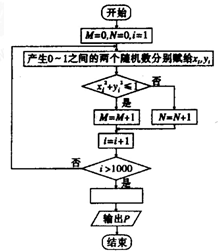 某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:
某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com