
 在直三棱柱ABC-A1B1C1中,已知∠BCA=90°,∠BAC=60°,AC=4,E为AA1的中点,点F为BE的中点,点H在线段CA1上,且A1H=3HC,则线段FH的长为( )
在直三棱柱ABC-A1B1C1中,已知∠BCA=90°,∠BAC=60°,AC=4,E为AA1的中点,点F为BE的中点,点H在线段CA1上,且A1H=3HC,则线段FH的长为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | $\sqrt{13}$ | D. | 3 |
分析 以C为原点建立空间直角坐标系,则C(0,0,0),A(0,4,0),B(0,4$\sqrt{3}$,0),E(4,0,m),A1(4,0,2m).可得F(2,2$\sqrt{3}$,$\frac{m}{2}$),H(1,0,$\frac{m}{2}$),利用空间两点间的距离公式计算即可.
解答 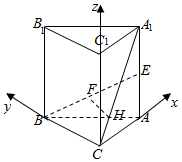 解:如图,以C为原点建立空间直角坐标系,
解:如图,以C为原点建立空间直角坐标系,
∵∠BCA=90°,∠BAC=60°,AC=4,∴BC=4$\sqrt{3}$,
则C(0,0,0),A(0,4,0),B(0,4$\sqrt{3}$,0),E(4,0,m),A1(4,0,2m).
∵点F为BE的中点,∴F(2,2$\sqrt{3}$,$\frac{m}{2}$),
∵点H在线段CA1上,且A1H=3HC,∴H(1,0,$\frac{m}{2}$)
∴FH=$\sqrt{(2-1)^{2}+(2\sqrt{3}-0)^{2}+(\frac{m}{2}-\frac{m}{2})^{2}}$=$\sqrt{13}$.
故选C.
点评 本题考查了空间两点间的距离公式计算,属于基础题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
| 公园 | 甲 | 乙 | 丙 | 丁 |
| 获得签名人数 | 45 | 60 | 30 | 15 |
| 有兴趣 | 无兴趣 | 合计 | |
| 男 | 25 | 5 | 30 |
| 女 | 15 | 15 | 30 |
| 合计 | 40 | 20 | 60 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | B盒中编号为奇数的小球与C盒中编号为偶数的小球一样多 | |
| B. | B盒中编号为偶数的小球不多于C盒中编号为偶数的小球 | |
| C. | B盒中编号为偶数的小球与C盒中编号为奇数的小球一样多 | |
| D. | B盒中编号为奇数的小球多于C盒中编号为奇数的小球 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -3或3 | D. | 2或$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com