
���� �����������������ͼ�ĸ������������ͼ����Сͼ�������ͼ�Σ��������ͼ����������ɵõ���ȷ���⣮
��� �⣺����������ABCD������ͼ��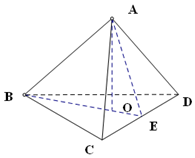
������ƽ���ڵ���BCD����CD����ʱ������ͼΪͼ�С�ABE��
�������Ϊ$\frac{1}{2}��2��\frac{\sqrt{3}}{2}��\sqrt{{2}^{2}-��2��\frac{\sqrt{3}}{3}��^{2}}$=$\sqrt{2}$���ʢ���ȷ��
������ƽ���ڵ���BCD����CO����ʱ��
����ͼΪ��BDΪ�ף���������ĸ�AOΪ�ߵ������Σ�
�������Ϊ$\frac{1}{2}��2��\sqrt{{2}^{2}-��2��\frac{\sqrt{3}}{3}��^{2}}$=$\frac{2\sqrt{6}}{3}$���ʢ���ȷ��
�����ߴ�ֱ�ڵ���BCDʱ������ͼΪ��BCD��
�����Ϊ$\frac{1}{2}��2��\sqrt{3}=\sqrt{3}$���ʢ���ȷ��
��������������������У�������ͼ��
���ߴ�ֱ���������������ǵ���ʱ������ͼ�������Σ�
�����Ϊ$\sqrt{2}��\sqrt{2}$=2�����Ҵ�ʱ����ͼ�����ʢ���ȷ���ݲ���ȷ��
�ʴ�Ϊ���٢ڢۢܣ�
���� ���⿼�鼸���������ͼ��Ӧ�ã��ܹ��ж�����ͼ�е�����ͼ����ֵͼ���ǽ�����ѵ�Ҳ�ǹؼ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b��c��a | B�� | b��a��c | C�� | a��b��c | D�� | a��c��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com