Question

6．已知f（x）=$\left\{\begin{array}{l}{ln（1-x），x＜0}\\{{x}^{2}-ax，x≥0}\end{array}\right.$，且g（x）=f（x）+$\frac{x}{2}$有三个零点，则实数a的取值范围为（　　）

• A． （$\frac{1}{2}$，+∞）
• B． [1，+∞）
• C． （0，$\frac{1}{2}$ ）
• D． （0，1]

Answer 1

分析 根据图象得出g（x）在（-∞，0）上的零点个数，得出g（x）在[0，+∞）上的零点个数，利用二次函数的性质得出a的范围．

解答 解：令g（x）=0得f（x）=-$\frac{x}{2}$，
作出f（x）=ln（1-x）与y=-$\frac{x}{2}$的函数图象，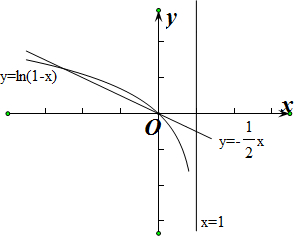

由图象可知f（x）与y=-$\frac{x}{2}$在（-∞，0）上只有1个交点，
∴g（x）=0在（-∞，0）上只有1个零点，
∴f（x）=-$\frac{1}{2}x$在[0，+∞）上有2个零点，即得到x²-ax+$\frac{x}{2}$=0在[0，+∞）上有两解，
解方程x²-ax+$\frac{x}{2}$=0得x₁=0，x₂=a-$\frac{1}{2}$，
∴a-$\frac{1}{2}$＞0，即a$＞\frac{1}{2}$．
故选A．

点评 本题考查了函数零点与函数图象的关系，属于中档题．