
| A. | 2 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 根据抛物线和双曲线有相同的焦点求得c=2,根据抛物线的定义可以求出P的坐标,运用双曲线的定义求得2a=2,然后求得离心率e.
解答 解:抛物线y2=8x焦点F(2,0),准线方程为x=-2,
设P(m,n),
由抛物线的定义可得|PF|=m+2=5,
解得m=3,
则n2=24,即有P(3,±2$\sqrt{6}$),
可得左焦点F'为(-2,0),
由双曲线的定义可得2a=|PF'|-|PF|=$\sqrt{25+24}$-$\sqrt{1+24}$=7-5=2,即a=1,
即有e=$\frac{c}{a}$=2.
故选A.
点评 本题主要考查了双曲线,抛物线的定义和简单性质,主要考查了离心率的求法,解答关键是利用抛物线和双曲线的定义.


科目:高中数学 来源: 题型:选择题
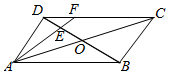 在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4-3i | B. | 4+3i | C. | -5+3i | D. | 3+4i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{9}$,9] | B. | (-∞,$\frac{1}{9}$] | C. | [$\frac{1}{2}$,2] | D. | (0,$\frac{1}{9}$]∪[9,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2log2x,$g(x)={log_2}{x^2}$ | B. | f(x)=|x|,$g(x)={(\sqrt{x})^2}$ | ||
| C. | f(x)=x,$g(x)=lo{g_2}{2^x}$ | D. | f(x)=x+1,$g(x)=\frac{x^2}{x}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com