
| A. | 3 | B. | $\sqrt{2}+1$ | C. | 2 | D. | $\sqrt{3}$ |
分析 先求解准线方程,代入双曲线方程求得y,根据双曲线的对称性可知△FAB为等腰直角三角形,进而可求得A或B的纵坐标为4,进而求得a,利用a,b和c的关系求得c,则双曲线的离心率可得.
解答 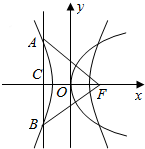 解:依题意知抛物线的准线x=-2,代入双曲线方程得
解:依题意知抛物线的准线x=-2,代入双曲线方程得
y=±$\frac{4}{a}$•$\sqrt{4-{a}^{2}}$,不妨设A(-2,$\frac{4}{a\sqrt{4-{a}^{2}}}$).
∵△FAB是等腰直角三角形,∴$\frac{4}{a\sqrt{4-{a}^{2}}}$=p=4,求得a=$\sqrt{2}$,
∴双曲线的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}+16}}{a}$=$\frac{\sqrt{18}}{\sqrt{2}}$=3,
故选:A.
点评 本题主要考查了双曲线的简单性质.解题的关键是通过双曲线的对称性质判断出△FAB为等腰直角三角形,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(1)+2f(1)+…+nf(1) | B. | f($\frac{n(n+1)}{2}$) | C. | n(n+1) | D. | n(n+1)f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
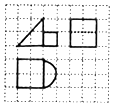
| A. | $\frac{8}{3}$+2π | B. | 4+4$\sqrt{2}$+3π | C. | 8+4$\sqrt{2}$+3π | D. | 10+4$\sqrt{2}$+2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
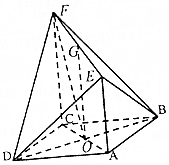 如图,四边形ABCD为菱形,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,G为EF中点.
如图,四边形ABCD为菱形,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF⊥平面ABCD,AB=AE=2,G为EF中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com