
| A. | $(\frac{15}{8},2]$ | B. | [2,+∞) | C. | $(-∞,\frac{15}{8}]$ | D. | $(\frac{15}{8},+∞)$ |
分析 方程有两个不等的实根可以转化为函数$y=\sqrt{-{x}^{2}-2x}$和函数y=kx+4的图象由两个不同的交点,在求出临界位置的直线的斜率即可.
解答 解:
方程有两个不等的实根等价于函数$y=\sqrt{-{x}^{2}-2x}$和函数y=kx+4的图象由两个不同的交点,
函数$y=\sqrt{-{x}^{2}-2x}$的解析式可变形为x2+y2+2x=0,即(x+1)2+y2=1(y≥0),其图象为圆点在(-1,0),半径为1的圆在x轴上方的部分,如图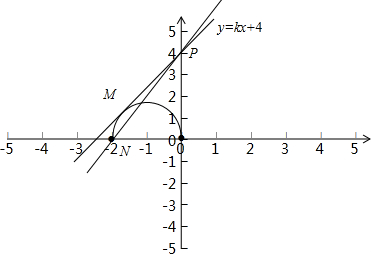
由图可知,当直线PN绕点P顺时针旋转至直线PM(PM为切线)位置时,直线与半圆有两个交点,
又${k}_{PN}=\frac{4-0}{0-(-2)}=2$,当直线与半圆相切时有:$\frac{|4-k|}{\sqrt{1+{k}^{2}}}=1$,解得:kPM=$\frac{15}{8}$,
∴k的取值范围是$(\frac{15}{8},2]$.
故选:A.
点评 本题考查用数形结合的方法判断方程解的个数问题.解题关键是能正确把方程得解的个数问题转化为函数图象的交点个数问题.此题若用代数方法求解要复杂得多.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 37 | B. | 38 | C. | 39 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某产品的广告费用x与销售额y的统计数据如表:
某产品的广告费用x与销售额y的统计数据如表:| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com