
【题目】下列函数中既是奇函数又在区间(﹣∞,0)上单调递增的函数是( )
A.y=![]() B.y=x2+1C.y=
B.y=x2+1C.y=![]() D.y=
D.y=![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(多选题)某工厂八年来某种产品总产量y(即前x年年产量之和)与时间x(年)的函数关系如图,下列五种说法中正确的是( )
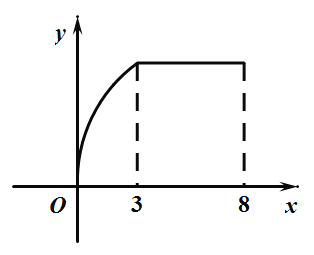
A.前三年中,总产量的增长速度越来越快
B.前三年中,总产量的增长速度越来越慢
C.前三年中,年产量的增长速度越来越慢
D.第三年后,这种产品停止生产
E.第三年后,年产量保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+2x,g(x)=x+ln x,h(x)=x-![]() -1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是________(由小到大).
-1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是________(由小到大).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD
为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD![]() 平面PBC=
平面PBC=![]() .
.
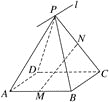
(1)求证:BC∥![]() ;
;
(2)MN与平面PAD是否平行?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱,现统计了连续![]() 天的售出和收益情况,如下表:
天的售出和收益情况,如下表:
售出水量 |
|
|
|
|
|
收益 |
|
|
|
|
|
(1)若每天售出![]() 箱水,求预计收益是多少元?
箱水,求预计收益是多少元?
(2)期中考试以后,学校决定将诚信用水的收益,以奖学金的形式奖励给品学兼优的特困生,规定:特困生考入年级前![]() 名,获一等奖学金
名,获一等奖学金![]() 元;考入年级前
元;考入年级前![]() 名,获二等奖学金
名,获二等奖学金![]() 元;考入年级
元;考入年级![]() 名以后的特困生不获得奖学金。甲、乙两名学生获一等奖学金的概率均为
名以后的特困生不获得奖学金。甲、乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() .
.
①在学生甲获得奖学金的条件下,求他获得一等奖学金的概率;
②已知甲、乙两名学生获得哪个等第的奖学金是相互独立的,求甲、乙两名学生所获得奖学金总金额![]() 的分布列及数学期望
的分布列及数学期望
附:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月24日,世界上最长的跨海大桥一港珠澳大桥正式通车![]() 在一般情况下,大桥上的车流速度
在一般情况下,大桥上的车流速度![]() 单位:千米
单位:千米![]() 时
时![]() 是车流密度
是车流密度![]() 单位:辆
单位:辆![]() 千米
千米![]() 的函数
的函数![]() 当桥上的车流密度达到220辆
当桥上的车流密度达到220辆![]() 千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆
千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆![]() 千米时,车流速度为100千米
千米时,车流速度为100千米![]() 时,研究表明:当
时,研究表明:当![]() 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
![]() Ⅱ
Ⅱ![]() 当车流密度x为多大时,车流量
当车流密度x为多大时,车流量![]() 单位时间内通过桥上某观测点的车辆数,单位:辆
单位时间内通过桥上某观测点的车辆数,单位:辆![]() 时
时![]() 可以达到最大?并求出最大值.
可以达到最大?并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com