
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{13}$ | C. | $\sqrt{14}$ | D. | 2$\sqrt{3}$ |
分析 求出双曲线方程的a,b,c,可得右焦点,即为抛物线的焦点,可得抛物线的方程,联立直线方程,可得x的二次方程,运用判别式大于0以及韦达定理和中点坐标公式,以及弦长公式求得AB的长,由点到直线的距离公式可得O到AB的距离,再由三角形的面积公式,计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{3}$-y2=1的a=$\sqrt{3}$,b=1,c=$\sqrt{3+1}$=2,
右焦点为(2,0),
则抛物线y2=2px(p>0)的焦点为(2,0),
即有2=$\frac{p}{2}$,解得p=4,即抛物线方程为y2=8x,
联立直线y=kx+m,可得k2x2+(2km-8)x+m2=0,
判别式△=(2km-8)2-4k2m2>0,
设A(x1,y1),B(x2,y2),可得x1+x2=$\frac{8-2km}{{k}^{2}}$,
点M(2,2)是AB的中点,
可得$\frac{8-2km}{{k}^{2}}$=4,且2=2k+m,
解得k=2,m=-2.满足判别式大于0.
即有x1+x2=4,x1x2=1,
可得弦长AB=$\sqrt{1+4}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{5}$•$\sqrt{16-4}$=2$\sqrt{15}$,
点O到直线2x-y-2=0的距离d=$\frac{|0-0-2|}{\sqrt{4+1}}$=$\frac{2}{\sqrt{5}}$,
则△OAB(O为坐标原点)的面积是$\frac{1}{2}$d•|AB|=$\frac{1}{2}$×$\frac{2}{\sqrt{5}}$×2$\sqrt{15}$=2$\sqrt{3}$.
故选:D.
点评 本题考查双曲线和抛物线的方程和性质,考查直线方程与抛物线的方程联立,运用韦达定理和中点坐标公式和弦长公式,考查点到直线的距离公式,以及三角形的面积公式的运用,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
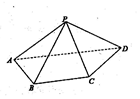 如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.
如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4i | B. | -4i | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(3,+∞) | B. | {x|x>3,x∈N} | C. | {4,8} | D. | [4,8] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {0,2} | C. | {1} | D. | {-1,1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
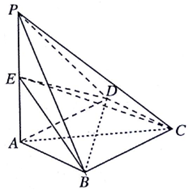 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com