考点:数列的求和,等差数列的通项公式,数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知得(6+5d)
2=(6+d)(6+13d),由此求出公差d=2,从而能求出a
n=2n+4.进而利用等比数列的通项公式列出方程组求出首项和公差,由此能求出b
n=2
n.
(Ⅱ)由S
n=n
2+5n,T
n=2
n+1-2,利用T
k>
,得
2k+1-2>,由此能求出使得T
k>
的最小k值.
解答:
解:(Ⅰ)由已知得(6+5d)
2=(6+d)(6+13d),
由d≠0,解得d=2,
∴a
n=6+(n-1)×2=2n+4.
∵a
1=6,a
2,a
6,a
14分别为等比数列{b
n}的第三、四、五项,
∴b
3=a
2=8,b
4=a
6=16,b
5=a
14=32,
∴
,解得b
1=2,q=2,
∴b
n=2
n.
(Ⅱ)S
n=6n+
×2=n
2+5n,
T
n=
=2
n+1-2,
∵T
k>
,∴
2k+1-2>,
整理,得2
k+2>k
2+5k+4,
解得k>2,∵k∈N
*,∴使得T
k>
的最小k值为3.
点评:本题主要考查数列的通项公式的求法、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、函数与方程思想,解题时要注意等价转化思想的合理运用.



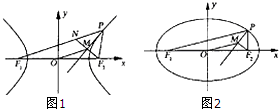 如图,P是双曲线
如图,P是双曲线