
分析 (Ⅰ)由曲线C1的参数方程,消去参数可得普通方程x2+y2=1,由于π≤α≤2π,可得-1≤x≤1,-1≤y≤0,即可得出直角坐标方程与极坐标方程.曲线C2的极坐标方程为ρ=2sinθ即ρ2=2ρsinθ,利用ρ2=x2+y2,y=ρsinθ,即可化为直角坐标方程.
(Ⅱ)设P(x0,y0),则-1≤y0≤0,直线l的倾斜角为α,可得直线l的参数方程为:$\left\{{\begin{array}{l}{x={x_0}+tcosα}\\{y={y_0}+tsinα}\end{array}}\right.$(t为参数).代入C2的直角坐标方程得t2+[2x0cosα+2sinα(y0-1)]t+1-2y0=0,由直线参数方程中t的几何意义可知|PM|•|PN|=|1-2y0|,即可得出.
解答 解:(Ⅰ)曲线C1的参数方程为$\left\{{\begin{array}{l}{x=cosα}\\{y=sinα}\end{array}}\right.$(α为参数,且α∈[π,2π]),消去参数可得x2+y2=1,
∵π≤α≤2π,∴-1≤x≤1,-1≤y≤0,
∴曲线C1是x2+y2=1在x轴下方(包括x轴上的两点)的部分,∴曲线C1的极坐标方程为ρ=1(π≤θ≤2π).
曲线C2的极坐标方程为ρ=2sinθ即ρ2=2ρsinθ,可得:曲线C2的直角坐标方程为x2+(y-1)2=1.
(Ⅱ)设P(x0,y0),则-1≤y0≤0,直线l的倾斜角为α,
则直线l的参数方程为:$\left\{{\begin{array}{l}{x={x_0}+tcosα}\\{y={y_0}+tsinα}\end{array}}\right.$(t为参数).
代入C2的直角坐标方程得${({x_0}+tcosα)^2}+{({y_0}+tsinα-1)^2}=1$,
即t2+[2x0cosα+2sinα(y0-1)]t+1-2y0=0,
由直线参数方程中t的几何意义可知|PM|•|PN|=|1-2y0|,
∵-1≤y0≤0,∴|PM|•|PN|∈[1,3].
点评 本题考查了极坐标与直角坐标方程的互化、参数方程化为普通方程、直线与圆相交、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
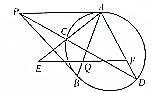 如图,过圆外一点P作圆的两条切线PA、PB,A,B为切点,再过P点作圆的一条割线分别与圆交于点C、D,过AB上任一点Q作PA的平行线分别与直线AC、AD交于点E,F,证明:QE=QF.
如图,过圆外一点P作圆的两条切线PA、PB,A,B为切点,再过P点作圆的一条割线分别与圆交于点C、D,过AB上任一点Q作PA的平行线分别与直线AC、AD交于点E,F,证明:QE=QF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com